Ulteriori informazioni su questo grafico di equazioni lineari

Le linee grafiche sono un'abilità fondamentale e questa calcolatrice ti aiuterà in questo. È necessario iniziare fornendo il file equazione lineare vuoi rappresentare graficamente.

Puoi fornire qualsiasi equazione lineare in modo esplicito, ad esempio x + 3y = 2 o qualcosa che non è completamente semplificato come x + 3y = 2/3 x.

Linee grafiche ha così tante applicazioni, che diventa un'abilità molto pratica da acquisire. Dal punto di vista geometrico, le linee hanno un'intuizione molto semplice che rende facile la rappresentazione grafica poiché non abbiamo bisogno di molte informazioni per specificarle.

Come rappresentare graficamente le equazioni lineari?

Puoi usare questo calcolatrice grafica per rappresentare graficamente le linee. Se scegli di farlo manualmente, devi essere consapevole che l'approccio richiede un preambolo che dipenderà dal tipo di informazioni fornite.

Quali sono i passaggi per rappresentare graficamente una linea?

• Passaggio 1: identificare il tipo di informazioni fornite. Hai un'equazione reale fornita, hai due punti, un punto e la pendenza, la pendenza e l'intercetta y? Valutalo chiaramente
• Passaggio 2: indipendentemente dalle informazioni fornite, utilizzale per trovare due punti in cui passa la linea. Per un'equazione data, risolvi per y per x = 0 e x = 1 per esempio. Per pendenza e intercetta y costruisci l'equazione y = a + bx e trova due punti. Se hai un punto e una pendenza, definisci y = y1 + b(x-x1) e collegalo a x = 0
• Passaggio 3: una volta che hai due punti in cui passa la linea, usa un righello per tracciare una linea che li attraversa

Le linee sono semplicissime da tracciare, devi solo essere metodico ed essere consapevole del tipo di informazioni che hai a disposizione.

Anche se lo fai a mano, è sempre bello avere un lineare a portata di mano calcolatrice grafica online per controllare i risultati.

Linee grafiche

Le linee grafiche hanno così tante applicazioni. Ad esempio, puoi risolvere un sistema di equazioni rappresentando graficamente le linee corrispondenti e vedendo dove si intersecano.

Usando quel metodo, quando le linee sono parallele e non si intersecano, non ci saranno soluzioni.

Simile a quanto è successo con l'addizione e la sottrazione, la divisione delle frazioni è semplicemente derivata dalla moltiplicazione delle frazioni: per dividere due frazioni, devi semplicemente moltiplicare la prima per il frazione inversa della seconda (la frazione inversa si ottiene scambiando il numeratore con il denominatore nella frazione).

Altre applicazioni dei grafici lineari

Linee o Grafici lineari sono davvero presenti ovunque. funzioni lineari compaiono sempre nelle applicazioni, in Calcolo e Ottimizzazione, quindi sono veramente utili.

Esempio: esempio di grafico a equazione lineare

Rappresenta graficamente le seguenti equazioni: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Soluzione: Dobbiamo lavorare con la seguente equazione:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Lavorando prima con le costanti:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Il risultato si ottiene ponendo (y) a sinistra e (x) e la costante a destra:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Quindi il processo continua risolvendo per \(y\), quindi dividendo entrambi i lati dell'equazione per \(\frac{7}{4}\). Otteniamo quindi:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

e dopo la semplificazione, il risultato è il seguente.

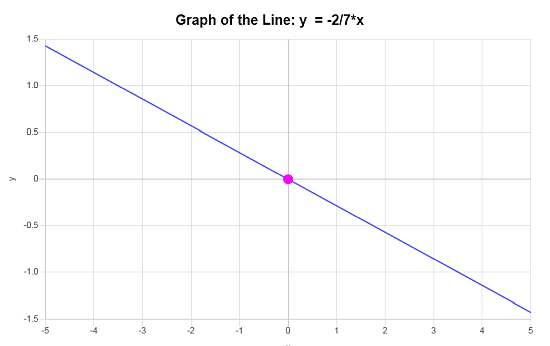
\[\displaystyle y=-\frac{2}{7}x\]

Conclusione : Deduciamo che l'equazione della retta in forma di intercetta pendenza che si basa sui dati disponibili è \(\displaystyle y=-\frac{2}{7}x\), con pendenza di \(\displaystyle b = -\frac{2}{7}\) e intercetta di y di \(\displaystyle n = 0\).

Quindi, il grafico della linea fornita è

Esempio: esempio di grafico a equazione lineare

Ottieni la riga che rappresenta: \(\frac{2}{3}x + \frac{5}{4}y = - \frac{5}{6}x + 2\)

Soluzione: Ci è stata fornita la seguente equazione:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Lavorando con le costanti:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Ora, mettendo \(y\) a sinistra e \(x\) e la costante a destra otteniamo

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Ora, il termine moltiplicando \(y\) è \( \frac{5}{4} - 0 = \frac{5}{4}\), e poichè \( -\frac{5}{6} - \frac{2}{3} = -\frac{3}{2}\) si ottiene quanto segue

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Ora, risolvendo per \(y\), dividendo entrambi i lati dell'equazione per \(\frac{5}{4}\), si ottiene quanto segue

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

e semplificando si ottiene la seguente formula

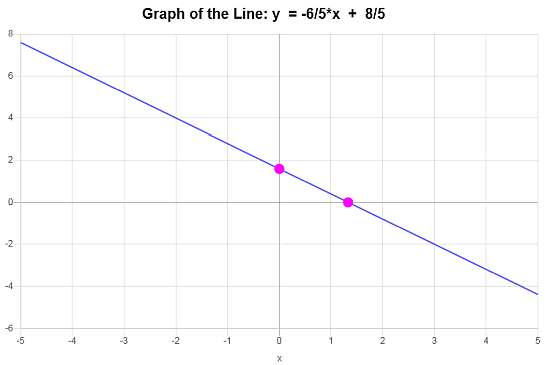
\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Conclusione : Sulla base dei dati forniti, concludiamo che l'equazione della retta in forma di intercetta pendenza è \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), con una pendenza di \(\displaystyle b = -\frac{6}{5}\) e y-intercetta di \(\displaystyle n = \frac{8}{5}\).

Il grafico lineare è

Altri calcolatori di linea

Le linee sono così importanti che meritano una sezione a parte nel libro della matematica. Puoi calcolare Equazioni lineari in forme diverse, a seconda delle specifiche esigenze.

Alla fine sarà necessario determinare le linee due punti in cui la retta passa per , che può essere data direttamente o indirettamente.