Statistiques non paramétriques, ou que faire lorsque les hypothèses d'un test paramétrique échouent

La moyenne, la médiane et le mode sont les mesures les plus courantes de la tendance centrale, utilisées pour décrire le centre d'une distribution. Sur les trois, la moyenne est la plus couramment utilisée, mais la médiane et le mode sont également largement utilisés.

Nous devons faire la distinction entre les échantillon moyenne, médiane et mode, et leur population homologues.

Typiquement, nous sommes fourni avec un échantillon et nous devons calculer la moyenne de l'échantillon, la médiane de l'échantillon et le mode d'échantillonnage. Ces statistiques sont estimateurs des paramètres de population correspondants.

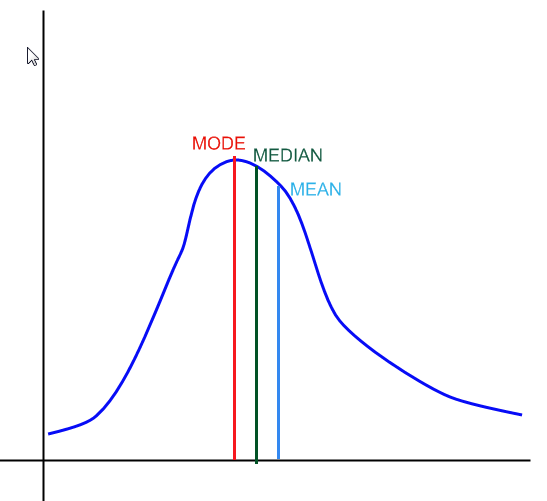
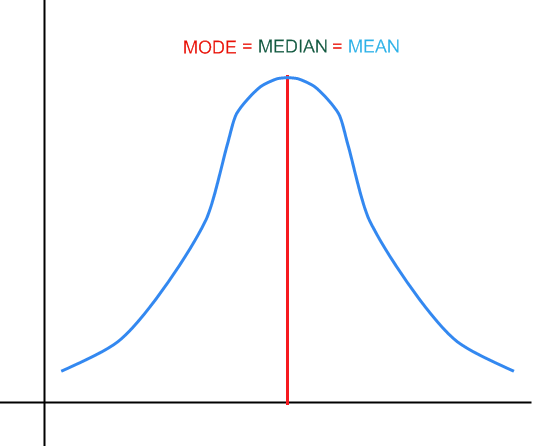
Dans le graphique ci-dessus, vous avez un exemple de l'apparence de la médiane, du mode et de la moyenne dans une distribution.

Le mode correspond à la valeur la plus répétée dans un échantillon. Dans une distribution, il correspond au point le plus élevé de la fonction de densité, comme indiqué dans le graphique ci-dessus.

La médiane, en gros, définit le point où 50% de la distribution se trouve à gauche et à droite de celle-ci.

La moyenne correspond à la moyenne pondérée des valeurs que prend la variable et de leurs probabilités associées ($\sum x \cdot p(x)$). Pour une distribution, cette somme pondérée est soit une somme, soit une intégrale. Pour un échantillon, nous calculons simplement la moyenne des valeurs de l'échantillon.

Comment calculer la moyenne, la médiane et le mode pour un échantillon donné

Supposons maintenant que l'on nous donne un échantillon $X_1, X_2, ..., X_n$, et que nous voulons calculer le mode, la médiane et la moyenne. Comment allons-nous procéder?

• Pour le mode: Facile. On trouve juste le nombre le plus répété. Ex: Si nous avons un échantillon 1, 2, 2, 2, 3, 1, 4, le mode est 2, car 2 est la valeur la plus répétée (elle est répétée 3 fois)

• Pour la médiane: Ce calcul est légèrement plus complexe. Prenez votre échantillon $X_1, X_2, ..., X_n$ et la première étape consiste à le réorganiser par ordre croissant. Supposons donc que $\hat X_1, \hat X_2, ..., \hat X_n$ soit l'échantillon après l'avoir réorganisé des valeurs les plus basses aux valeurs les plus élevées.

Maintenant, nous allons calculer la position de la médiane dans l'échantillon par ordre croissant. Pour la taille de l'échantillon $n$, nous calculons $P = 0.5 (n+1)$.

Si cette valeur est un entier, alors nous trouvons que la médiane est la valeur dans le P ^e position dans l'échantillon par ordre croissant.

Si cette valeur n'est PAS un entier, alors nous trouvons $P_L$ et $P_U$ qui sont les entiers les plus proches à gauche et à droite de $P$. (Ex: Si $P = 10.2$, alors $P_L = 10$ et $P_U = 11$).

Ensuite, la médiane est la moyenne des valeurs qui sont dans les positions $P_L$ ^e et $P_U$ ^e dans l'achat par ordre croissant. Ne vous inquiétez pas, nous allons pratiquer cela avec un exemple.

• Pour la moyenne: Simple aussi. La moyenne de l'achat est évaluée à l'aide de la formule

\[\displaystyle \frac{1}{n}\sum_{i=1}^n X_i\]

EXEMPLE 1

Trouvez la moyenne, la médiane et le mode pour l'exemple suivant:

28, 36, 43, 30, 15, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 12 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51

RÉPONDRE:

Le tableau suivant montre les calculs nécessaires pour calculer la moyenne

	Les données
	28
	36
	43
	30
	15
	19
	46
	36
	34
	38
	42
	29
	37
	35
	39
	39
	30
	39
	36
	38
	30
	41
	42
	46
	40
	33
	30
	40
	43
	12
	42
	39
	30
	35
	38
	41
	30
	37
	40
	30
	30
	35
	39
	37
	42
	42
	37
	38
	32
	51

Somme =	1791
Moyenne =	35,82

La moyenne de l'achat est donc

\[\bar{X}=\frac{1}{n}\sum{{{X}_{i}}}=\frac{1791}{50}=35.82\]

Maintenant, pour la médiane, le tableau suivant montre les données dans l'ordre croissant:

Données (par ordre croissant)
12
15
19
28
29
30
30
30
30
30
30
30
30
32
33
34
35
35
35
36
36
36
37
37
37
37
38
38
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
43
43
46
46
51

Dans ce cas, la position de la médiane est P = 0,5 * (50 + 1) = 25,5, donc alors ${{P}_{L}}=25$ et ${{P}_{U}}=26$. La valeur en position 25 ^e dans les données par ordre croissant est 37, et la valeur en position 26 est 37 également. La médiane est alors

\[Median=\frac{{37}+{37}}{2}=37\]

Le mode, qui est la valeur la plus répétée, est 30.

Qu'est-ce qui est le plus grand, la moyenne, la médiane ou le mode?

C'est une question qui revient fréquemment. En termes généraux, il n'y a pas une seule réponse pour toutes les distributions. C'est, la réponse dépend de la distribution.

Pour une distribution symétrique, nous avons :

\[\Large \text{Mode} = \text{Median} = \text{Mean} \]

Graphiquement:

Moyenne, médiane et mode pour une distribution symétrique

Pour une distribution asymétrique à droite, nous avons :

\[\Large \text{Mode} \le \text{Median} \le \text{Mean} \]

Graphiquement:

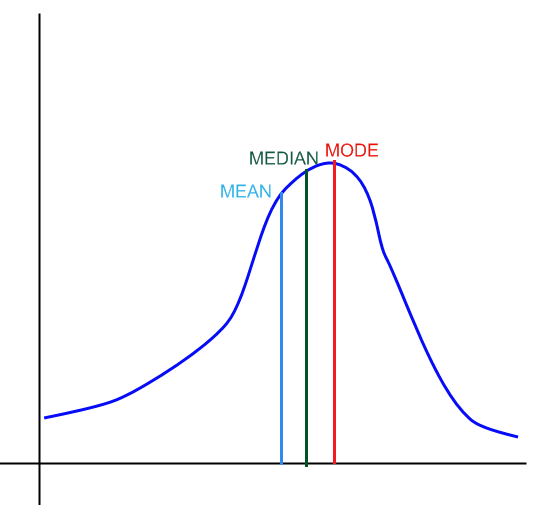
Pour une distribution asymétrique à gauche, nous avons :

\[\Large \text{Mean} \le \text{Median} \le \text{Mode} \]

Graphiquement:

Médiane, moyenne et mode pour une distribution asymétrique à gauche

En savoir plus sur la moyenne, la médiane et le mode

La médiane, la moyenne et le mode sont des concepts répandus qui sont utilisés partout dans les statistiques. Ils représentent des mesures de centre, qui tentent de donner une valeur représentative de l'achat.

Selon le niveau de mesure, nous utilisons une mesure différente du centre.

• Pour les données nominales, nous utilisons le mode.

• Pour les données ordinales non quantitatives, nous utilisons le mode ainsi que la mesure du centre.

• Pour les données ordinales et quantitatives, nous utilisons la médiane ou la moyenne comme mesure du centre.

• Pour les données d'intervalle et de rapport, nous utilisons la moyenne (ou la médiane si la distribution est trop asymétrique) comme mesure du centre.

Applications

La moyenne, la médiane et le mode sont les mesures de centre les plus utilisées. La moyenne et la médiane sont utilisées pour les données quantitatives et le mode est utilisé pour les données catégorielles.

Pour les données quantitatives, on utilisait généralement la moyenne. Avec une mise en garde: la moyenne est très sensible aux valeurs aberrantes. Cela signifie qu'une valeur aberrante (valeur légitime ou erreur de frappe) pourrait faire une différence drastique sur la valeur de la moyenne.

Dans de tels cas, lorsque y a des valeurs aberrantes ou que la distribution est assez asymétrique, il est préférable d'utiliser la médiane comme mesure la plus précise du centre, car la moyenne est déformée par l'asymétrie ou les valeurs aberrantes.

Un exemple de ceci est lorsque des échantillons sont collectés pour évaluer le revenu des réponses. Si nous prenons un échantillon de 100 personnes et que nous constatons que 99 d'entre elles gagnent 10000 dollars par an et qu'une personne gagne 100 millions de dollars par an, le revenu moyen de cet échantillon serait de (10000 * 99 + 1 * 100000000) / 100 = 1 009 900,00 $. Donc, en moyenne, tout le monde gagne 1 009 900,00 $, donc vous auriez l'idée que cet échantillon doit provenir d'une zone très aisée, mais ce n'est pas le cas: c'est juste une valeur aberrante qui déforme fortement la moyenne. En effet, dans ce cas, la médiane est de 10 000 $, ce qui est une valeur de centre beaucoup plus représentative pour cet échantillon.

Calculateurs associés

Si vous avez besoin de voir des solutions étape par étape pour le calcul de la moyenne et d'autres mesures de la tendance centrale, consultez calculateur de statistiques descriptives . Vous pouvez également trouver utile notre Calculatrice récapitulative à 5 chiffres .