Résumé en cinq chiffres

En savoir plus calculatrice de résumé à 5 chiffres pour vous permettre de mieux comprendre les résultats étape par étape fournis par cette calculatrice.

Comment calcule-t-on le résumé à 5 chiffres ?

La première chose que vous devez savoir, c'est quelles sont les parties d'un résumé à 5 chiffres, qui est l'une des techniques les plus courantes utilisées dans les statistiques descriptives.

Le résumé en cinq chiffres est un ensemble de cinq statistiques descriptives différentes qui vous donnent une vue rapide et précise de la distribution de l'échantillon de données que vous analysez.

Son calcul est un processus en plusieurs étapes, qui implique l'obtention de 5 éléments d'information. En effet, pour un ensemble d'échantillons de données, le résumé en cinq nombres est un ensemble de cinq nombres qui donne un aperçu rapide de la forme de la distribution. Le résumé en cinq chiffres comprend les éléments suivants minimum le premier quartile \((Q_1)\), La médiane le troisième quartile \((Q_3)\), et le maximum .

La Résumé en cinq chiffres peut vous renseigner sur le centre et l'étendue de la distribution de l'échantillon, ainsi que sur le type d'asymétrie (le cas échéant) et les valeurs aberrantes potentielles.

Étapes nécessaires pour le calcul du résumé à 5 chiffres

La façon de la trouver dépend de la manière dont vous voulez procéder, et vous verrez qu'il y a différentes façons de la calculer.

1. Si vous utilisez notre calculatrice, il vous suffit de fournir les données de l'échantillon et la calculatrice se chargera du travail en vous montrant toutes les étapes.
2. Si vous utilisez Excel, vous devrez calculer séparément chacune des composantes du résumé à 5 chiffres, car il n'existe pas de fonction spécifique pour les obtenir en une seule fois. Une petite chose à propos d'Excel est qu'il a tendance à utiliser une méthode simplifiée à l'extrême pour calculer les quartiles
3. Si vous le faites à la main, vous devez trier les données par ordre croissant. Ensuite, le premier chiffre sera le minimum et le dernier le maximum. La médiane et les quartiles sont calculés en utilisant une convention d'interpolation pour la position des valeurs dans la liste.

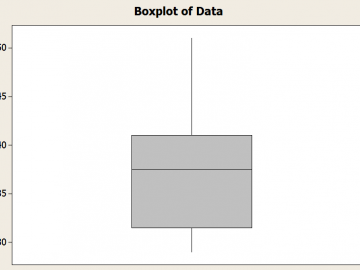
Le diagramme en boîte du résumé à 5 chiffres

Comment se présentent le résumé en 5 chiffres et le box plot en rapport ?. Il s'agit d'une relation très étroite, car le diagramme en boîte est essentiellement construit sur la base des 5 nombres.

En fait, les limites inférieures et supérieures de la boîte sont données par les paramètres suivants quartiles Q1 et Q3 les moustaches sont déterminées par le maximum et le minimum (bien qu'il y ait un plafond basé sur la valeur du valeur de l'IQR en utilisant le critère de 1,5 fois l'IQR)

Autres calculateurs de statistiques descriptives

En revanche, vous pouvez souhaiter obtenir une liste complète de statistiques descriptives, comprenant les mesures les plus courantes de la tendance centrale et de l'écart. Pour ce faire, vous pouvez suivre pas à pas les étapes suivantes calculatrice de statistiques descriptives

. De plus, le résumé en 5 nombres joue un rôle crucial dans la construction de l'image de marque de l'Union européenne diagramme en boîte qui en dit long sur la distribution d'un échantillon de données donné, ainsi que sur la distribution de l'échantillon de données détection des valeurs aberrantes .

Résumer

Le résumé en 5 chiffres est une collection de chiffres qui vous aide à dresser le portrait des mesures de tendance centrale et de dispersion à partir d'un échantillon de données donné. Les composants sont les suivants :

• Le minimum
• Le premier quartile
• La médiane
• Le troisième quartile
• le maximum

Exemple de résumé en cinq chiffres :

Question : Considérons l'échantillon de données suivant : 1, 1, 2, 3, 4, 4, 2, 3, 2, 1, 2, 3, 4, 5, 6, 6, 6, 2, 10, 11. Calculez le résumé en cinq nombres à la main, en montrant tous les calculs.

Solution :

Voici les exemples de données qui ont été fournis :

Observation	\(X\)
1	1
2	1
3	2
4	3
5	4
6	4
7	2
8	3
9	2
10	1
11	2
12	3
13	4
14	5
15	6
16	6
17	6
18	2
19	10
20	11

Voici les exemples de données qui ont été fournis :

Position	\(X\) (Asc. Order)
1	1
2	1
3	1
4	2
5	2
6	2
7	2
8	2
9	3
10	3
11	3
12	4
13	4
14	4
15	5
16	6
17	6
18	6
19	10
20	11

D'après le tableau ci-dessus, le minimum est \(\min = 1\) et le maximum est \(\max = 11\). La position du premier quartile \(Q_1\) est maintenant :

\[ L_{25} = \frac{25}{100} \times (n+1) = 0.25 \times 21 = 5.25 \]

Comme \( L_{25} = 5.25\) n'est pas un nombre entier, le premier quartile \(Q_1\) est calculé par interpolation entre les valeurs situées dans les positions \(5^{th}\) et \(6^{th}\), comme indiqué dans la formule ci-dessous :

\[ Q_1 = 2 + (5.25 - 5)\times (2 - 2) = 2\]

Comme la taille de l'échantillon \(n = 20\) est paire, nous savons que \((n+1)/2 = (20+1)/2 = 10.5\) n'est pas une valeur entière, de sorte que la médiane est calculée directement en trouvant la moyenne des valeurs situées aux positions \(10^{th}\) et \(11^{th}\), c'est-à-dire :

\[ median = \displaystyle \frac{3 + 3}{2} = 3.5\]

La position du troisième quartile \(Q_3\) est maintenant :

\[ L_{75} = \frac{75}{100} \times (n+1) = 0.75 \times 21 = 15.75 \]

Comme \( L_{75} = 15.75\) n'est pas un nombre entier, le troisième quartile \(Q_3\) est calculé par interpolation entre les valeurs situées dans les positions \(15^{th}\) et \(16^{th}\), comme indiqué dans la formule ci-dessous :

\[ Q_3 = 5 + (15.75 - 15)\times (6 - 5) = 5.75\]

Par conséquent, sur la base des résultats obtenus ci-dessus, nous obtenons le résumé suivant en cinq chiffres :

Minimum =	\(1\)
\(Q_1\) =	\(2\)
Median =	\(3.5\)
\(Q_3\) =	\(5.75\)
Maximum =	\(11\)