Diagramme en boîte et moustache
Le Box and Whisker Plot, ou également connu sous le nom de Box-plot, est un type de représentation graphique d'un échantillon, qui fournit des caractéristiques clés faciles à voir de la distribution d'un échantillon.
Un diagramme en boîtes et moustaches fournit la médiane ainsi que les premier et troisième quartiles dans sa «boîte», et le minimum et le maximum dans la «moustache».
Lorsque le minimum ou le maximum sont trop extrêmes, le "trim" la moustache et nous annotons l'existence d'une valeur aberrante.
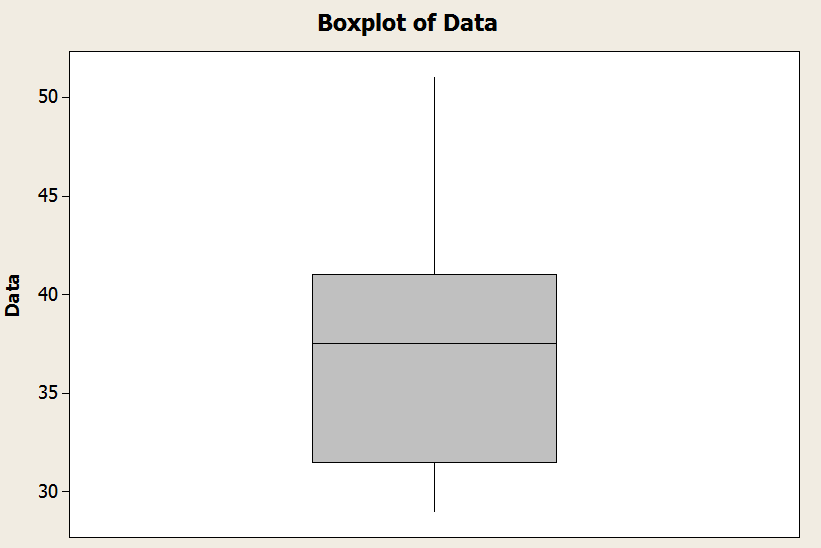
Dans le graphique ci-dessus, vous avez un exemple de l'apparence d'une boîte à moustaches: Vous avez la «boîte» et les moustaches.
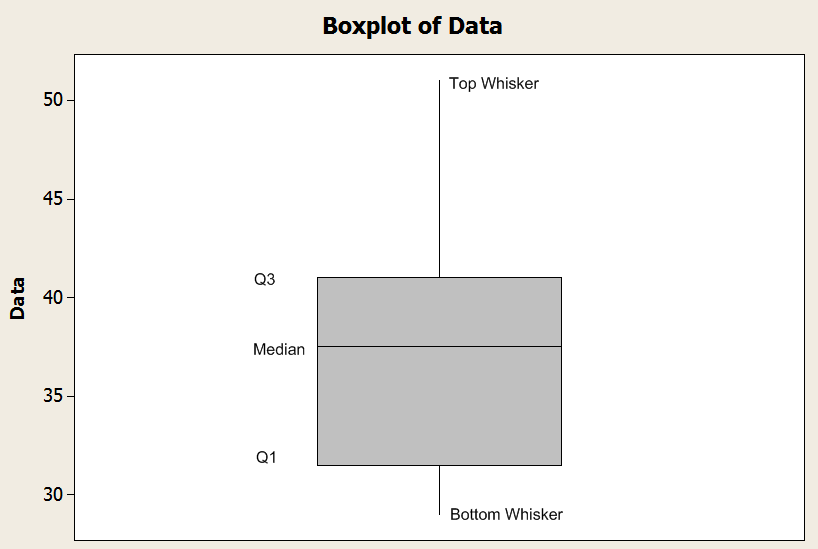
La ligne du bas de la boîte est définie par le premier quartile (\(Q_1\)).
La ligne médiane de la boîte est définie par la médiane (\(Q_2\)).
La ligne supérieure de la boîte est définie par le troisième quartile (\(Q_3\)).
Maintenant, pour les moustaches, il y a une règle à suivre: la moustache inférieure est définie par le minimum de l'échantillon, et la moustache supérieure est définie par le maximum de l'échantillon. Ceci est à condition que la taille de la moustache soit inférieure à \(1.5 \times IQR\), où \(IQR\) est l'intervalle interquartile, et il est défini par \(IQR = Q_3 - Q_1\).
Voir l'exemple de graphique ci-dessous.
Donc, si le minimum de l'échantillon est supérieur à \(Q_1 - 1.5 \times IQR\), alors la moustache inférieure est définie par le minimum. Sinon, il est défini par \(Q_1 - 1.5 \times IQR\).
De même, si le maximum de l'échantillon est inférieur à \(Q_3 + 1.5 \times IQR\), alors la moustache supérieure est définie par le maximum. Sinon, il est défini par \(Q_3 + 1.5 \times IQR\).
EXEMPLE 1
Construisez un box-plot pour l'exemple suivant:
28, 36, 43, 30, 46, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 30, 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51
RÉPONDRE:
Nous obtenons que le maximum et le minimum sont
\[\min = 19\] \[\max = 51\]Le tableau suivant présente les données par ordre croissant:
|
Données (par ordre croissant) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
51 |
La médiane est alors
\[Median=\frac{{37}+{38}}{2}=37.5\]La position du 25e centile est
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Ensuite, nous obtenons cela
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La position du 75e centile est
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Ensuite, nous obtenons cela
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Par conséquent, le résumé à 5 chiffres est
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 51\]Dans ce cas, l'intervalle interquartile est \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Par conséquent,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observez que le minimum est de 19 et qu'il est supérieur à \(Q_1 - 1.5 \times IQR = 17.25\). Et le maximum est de 51, et il est inférieur à \(Q_3 + 1.5 \times IQR = 55.25\).
Nous concluons que la moustache inférieure est le minimum, et la moustache supérieure est le maximum dans ce cas. Graphiquement
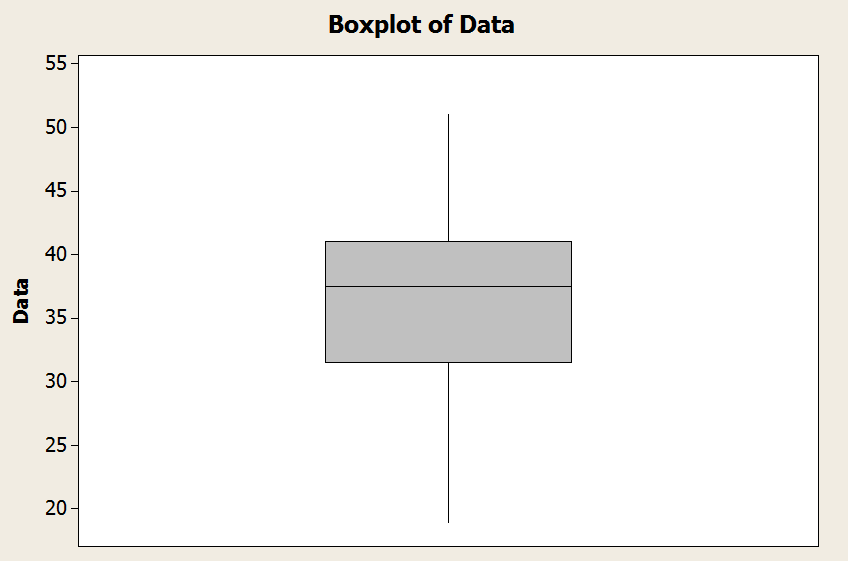
EXEMPLE 2
Recherchez la boîte à moustaches pour le même échantillon de l'exemple précédent, mais lorsque vous remplacez «51» par «81».
RÉPONDRE:
Nous obtenons que le maximum et le minimum sont
\[\min = 19\] \[\max = 81\]Le tableau suivant présente les données par ordre croissant:
|
Données (par ordre croissant) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
81 |
La médiane est alors
\[Median=\frac{{37}+{38}}{2}=37.5\]La position du 25e centile est
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Ensuite, nous obtenons cela
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La position du 75e centile est
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Ensuite, nous obtenons cela
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Par conséquent, le résumé à 5 chiffres est
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 81\]Dans ce cas, l'intervalle interquartile est \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Par conséquent,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Observez que le minimum est de 19 et qu'il est supérieur à \(Q_1 - 1.5 \times IQR = 17.25\). Mais maintenant, le maximum est de 81, ce qui dépasse \(Q_3 + 1.5 \times IQR = 55.25\). Par conséquent, la valeur «81» est une valeur aberrante.
Nous concluons que la moustache inférieure est le minimum et la moustache supérieure est définie par \(Q_3 + 1.5 \times IQR = 55.25\). Graphiquement
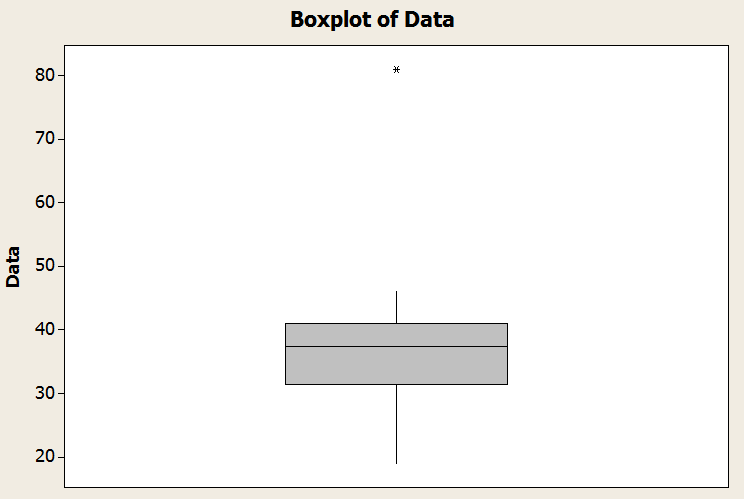
En savoir plus sur le Boxplot
La principale question que les gens se posent est ce que les boxplots vous disent. Que représentent-ils. Et la réponse est simple: ils vous donnent une représentation résumée de la distribution d'un échantillon en fournissant un graphique schématique montrant la position relative du Résumé à 5 chiffres .
De cette façon, vous pouvez rechercher valeurs aberrantes , vous pouvez évaluer le degré d'asymétrie de la distribution, et vous pouvez analyser rapidement les régions ayant 25%, 50% et 75% de la distribution totale.
Différence entre Box-plot et Histogramme
L'un des avantages de la boîte à moustaches est qu'il fournit des informations légèrement différentes de celles fournies par un histogramme.
En effet, l'histogramme montre la forme brute de la distribution, en fonction des classes utilisées pour classer les valeurs possibles de la variable aléatoire. D'autre part, le boxplot fournit des informations résumées sur les quartiles et le résumé à 5 chiffres, ce qui vous en dit long sur la position relative du premier et du troisième quartile par rapport à la médiane.
En d'autres termes, le boxplot, contrairement à l'histogramme, présente un graphique qui représente un résumé de la distribution , plutôt qu'une représentation brute. Les seules valeurs brutes qui iraient dans une boîte à moustaches seraient les valeurs aberrantes (s'il y en a).
Applications
L'application la plus classique du box plot est la détection des valeurs aberrantes. Par définition, le box-plot limite la taille des moustaches à 1,5 fois l'intervalle interquartile \((IQR)\) à partir des extrémités de la boîte (qui sont définies par \(Q_1\) et \(Q_3\).
Ainsi, tous les points qui dépassent la taille maximale des moustaches seront annotés dans la boîte à moustaches et ils seront considérés comme une valeur aberrante.
Mettez en pratique les concepts que vous avez appris dans ce didacticiel en utilisant ce fabricant de box-plot . Un autre créateur de graphes qui permettra de voir en un coup d'œil les propriétés distributionnelles de la distribution d'un échantillon est ce créateur d'histogramme , ou ca fabricant de parcelles à tige et feuille .