Inégalités de valeur absolue
Les inégalités de valeur absolue sont des inégalités dans lesquelles il y a un ou plusieurs valeur absolue . Rappelons qu'une inégalité est presque comme une équation, mais au lieu du signe "=", nous avons "≤" ou "≥".
Cette différence fait que l'ensemble de solutions est généralement une région, comme pour la plupart des inégalités. Et le fait qu'il y ait des valeurs absolues impliquées indique un certain traitement particulier pour leur résolution.
Dans ce tutoriel, nous nous concentrerons sur les compétences spécifiques requises pour la résolution de ce type d'inégalité qui contient une ou plusieurs valeurs absolues. De plus, nous supposerons qu'une ou deux variables, \(x\) et / ou \(y\) sont impliquées dans l'inégalité.
Qu'est-ce qu'une inégalité de valeur absolue?
Pour les besoins de cette analyse, nous considérerons une inégalité de valeur absolue comme une inégalité impliquant une ou deux variables, avec au moins une valeur absolue.
Par exemple, ci-dessous, nous avons une inégalité de valeur absolue avec deux variables \(x\) et \(y\):
\[|3x+2y-1| \ge 1\]Ou aussi, nous pourrions avoir l'inégalité de valeur absolue suivante avec une seule variable:
\[|3x-1| \le 2\]Pour nos besoins, et pour les besoins des techniques utilisées pour leur résolution, nous traiterons les deux types d'inégalités (une et deux variables)
Comment résoudre les inégalités de valeur absolue?
Lors de la résolution d'équations ou d'inégalités, il n'existe pas vraiment de solution miracle pour tout résoudre. Chaque problème est différent et peut avoir ses propres particularités.
Le mieux que nous puissions faire est de fournir une série d'étapes qui vous aideront dans le processus de résolution d'une inégalité.
Étape 1:
Pour chaque absolu, déterminez les régions dans lesquelles l'argument de la valeur absolue est négatif et où il est non négatif.
Étape 2:
S'il n'y a qu'une seule valeur absolue dans l'inégalité, résolvez-la dans les deux domaines (où l'argument de la valeur absolue est négatif et où il est non négatif).
Étape 3:
S'il y a plus d'une valeur absolue dans l'inégalité, vous devez intersecter toutes les régions afin d'obtenir un ensemble de partitions plus petites. Dans chaque partition, vous devez connaître EXACTEMENT le signe de chaque argument. Ensuite, résolvez les inégalités dans tous les domaines.
Étape 4:
Une fois que vous avez obtenu la solution de pièce qui se trouve dans chacun des domaines, la solution finale est simplement l'union de ces solutions de pièce.
En termes simples: vous devez trouver les régions où vous connaissez exactement le signe de l'argument des valeurs absolues (afin de pouvoir vous en débarrasser).
Quelques exemples devraient clarifier ces étapes.
EXEMPLE 1
Résolvez l'inégalité suivante
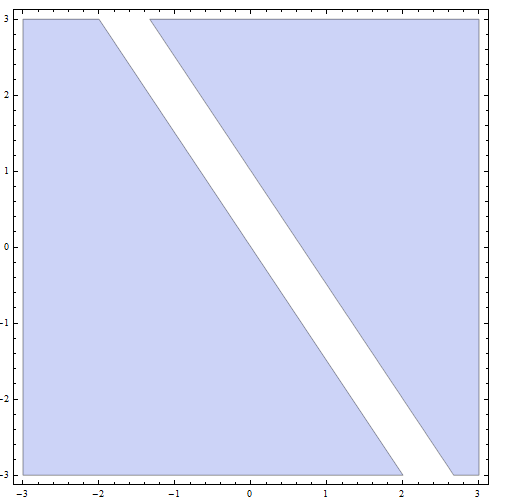
\[| 2x + 4y - 1 | \ge 2\]RÉPONDRE:
Afin de résoudre l'inégalité, nous devons utiliser les étapes spécifiées ci-dessus.
Étape 1: Il n'y a qu'une seule valeur absolue, nous devons donc déterminer si l'argument est négatif et non négatif. Par conséquent, nous devons d'abord résoudre:
\[2x + 4y - 1 \ge 0\]Il existe plusieurs stratégies pour résoudre ce qui précède, mais la plus simple consiste à résoudre d'abord l'équation
\[2x + 4y - 1 = 0\]ce qui signifie que \(4y = -2x + 1\) ou le même que \(y = -\frac{1}{2}x + \frac{1}{4}\), ce qui correspond à une ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = \frac{1}{4}\).
Maintenant, pour prendre soin de \(2x + 4y - 1 \ge 0\) nous testons si le point \((0,0)\) satisfait ou non l'inégalité:
\[2(0) + 4(0) - 1 = -1 < 0\]Ainsi, \((0,0)\) satisfait ou non l'inégalité. La conclusion est que la droite avec la pente \(m = -\frac{1}{2}\) et l'ordonnée à l'origine \(n = \frac{1}{4}\) divise le plan en deux régions:
Pour les points en dessous de la ligne (nous appelons cette région 1, \(R_1\)), nous obtenons que \(2x + 4y - 1 < 0\)
Pour les points au-dessus de la ligne, y compris la ligne elle-même (nous appelons cette région 2, \(R_2\)), nous obtenons que \(2x + 4y - 1 \ge 0\)
Pourquoi est-ce important? Pourquoi nous prenons tout ce problème? Parce que sur \(R_1\), nous obtenons cela depuis \( 2x + 4y - 1 < 0\), puis \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). De même, sur \(R_2\), nous obtenons cela depuis \( 2x + 4y - 1 \ge 0\), puis \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Étape 2: Nous devons maintenant résoudre l'inégalité sur la région 1, \(R_1\) :
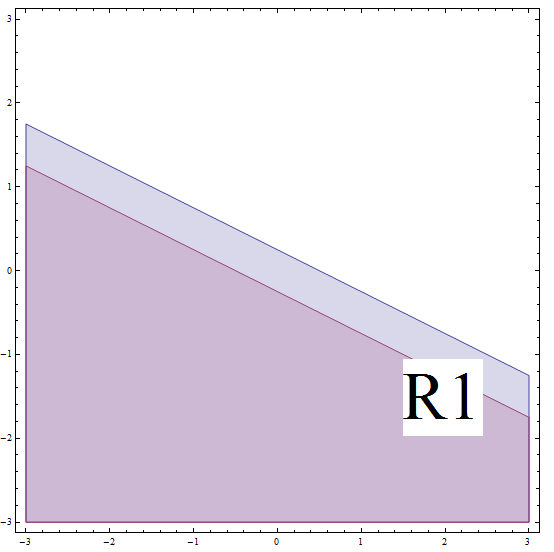
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Cela correspond à tous les points ci-dessous ou sur la ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = -\frac{1}{4}\). Mais n'oubliez pas que vous êtes sur \(R_1\), et cette ligne que nous avons trouvée est AU-DESSOUS de la limite de \(R_1\) (voir le graphique ci-dessous).
Pour clarifier, puisque nous sommes sous l'hypothèse que nous sommes dans \(R_1\), nous devons avoir que nous sommes en dessous de la ligne avec la pente \(m = -\frac{1}{2}\) et l'ordonnée à l'origine \(n = \frac{1}{4}\). Sous cette hypothèse, nous avons résolu l'inégalité d'origine et nous devons également être en dessous de la ligne avec la pente \(m = -\frac{1}{2}\) et l'ordonnée à l'origine \(n = -\frac{1}{4}\). Ces deux conditions doivent se produire simultanément, nous obtenons donc l'intersection des deux régions.
Ainsi donc, la solution de la partie dans ce cas correspond à tous les points en dessous ou sur la ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = -\frac{1}{4}\).
Nous devons maintenant résoudre l'inégalité sur la région 2, \(R_2\) :
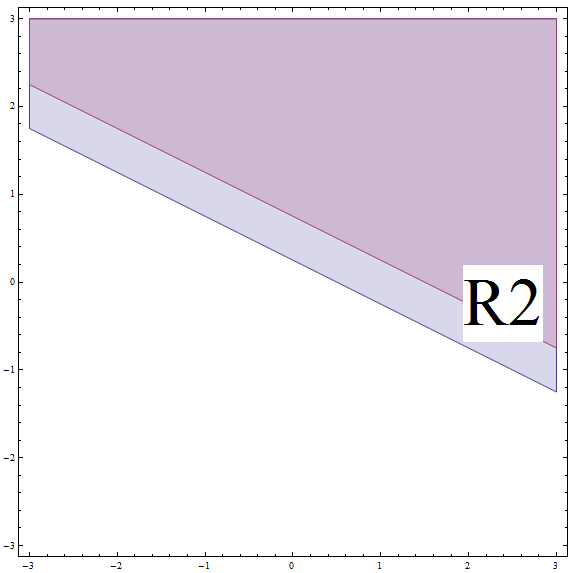
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Cela correspond à tous les points au-dessus ou sur la ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = \frac{3}{4}\). Mais n'oubliez pas que vous êtes sur \(R_2\), et que cette ligne est AU-DESSUS de la limite de\(R_2\) (voir le graphique ci-dessous).
En trouvant l'intersection entre \(R_2\) et la région ci-dessus, nous obtenons que la solution partielle dans ce cas est tous les points au-dessus ou sur la ligne avec la pente \(m = -\frac{1}{2}\) et l'ordonnée à l'origine \(n = \frac{3}{4}\).
Étape 4: Maintenant, la solution finale est l'union de toutes les solutions des parties des parties précédentes: La solution finale est tous les points CI-DESSOUS ou sur la ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = -\frac{1}{4}\), PLUS tous les points AU-DESSUS ou sur la ligne avec pente \(m = -\frac{1}{2}\) et ordonnée à l'origine \(n = \frac{3}{4}\).
Graphiquement, nous obtenons
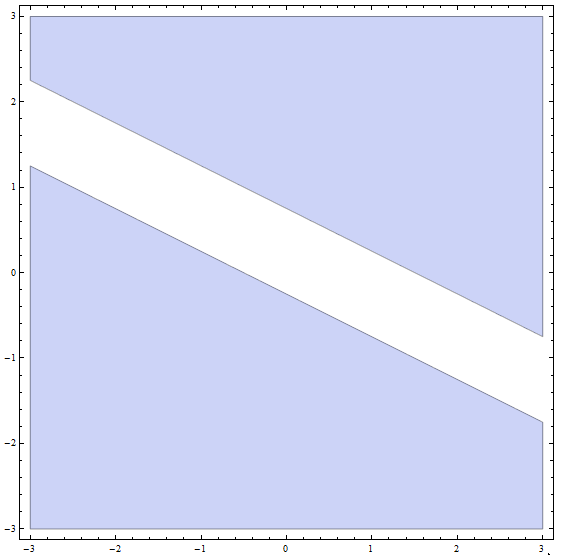
ce qui conclut la résolution de l'inégalité.
EXEMPLE 2
Résoudre la double inégalité de valeur absolue suivante
\[| 2x - 1 | \ge |x + 3|\]RÉPONDRE:
Il s'agit d'une double inégalité de valeur absolue car il y a 2 valeurs absolues. Cela signifie que trouver les régions demandera un peu plus de travail (relativement parlant).
Étape 1: Pour la première valeur absolue, nous résolvons:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Nous obtenons donc ce \(2x- 1 \ge 0\) sur \([\frac{1}{2}, +\infty)\) et \(2x- 1 < 0\) sur \((-\infty, \frac{1}{2})\).
Pour la deuxième valeur absolue, nous résolvons:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Nous obtenons donc ce \(x+3 \ge 0\) sur \([-3, +\infty)\) et \(x+3 < 0\) sur \((-\infty, -3)\).
Alors, nous définissons 4 régions:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). Sur cette région, nous obtenons: \(2x- 1 \ge 0\) ET \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). Sur cette région, nous obtenons: \(2x- 1 \ge 0\) AND \(x+3 < 0\), bien que cette région soit vide.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). Sur cette région, nous obtenons: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). Sur cette région, nous obtenons: \(2x- 1 < 0\) ET \(x+3 < 0\).
Étape 2: Nous devons maintenant résoudre la double inégalité de valeur absolue sur chacune des quatre régions:
• Le \(R_1\):
Ici, nous obtenons \(2x- 1 \ge 0\) ET \(x+3 \ge 0\) donc alors
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Donc, pour obtenir la solution partielle, nous devons intersecter \(x \ge 4\) ou \([4, +\infty)\) avec \(R_1\).
La solution de pièce correspondante est donc: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• Le \(R_2\):
Cette solution partielle est vide (\(\varnothing\)).
• Le \(R_3\):
Ici, nous obtenons \(2x- 1 < 0\) ET \(x+3 \ge 0\) donc alors
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Donc, pour obtenir cette solution partielle, nous devons intersecter \( x \le -\frac{2}{3}\), ou \( (-\infty, -\frac{2}{3}]\) avec \(R_3\).
La solution de pièce correspondante est donc: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• Le \(R_4\):
Ici, nous obtenons \(2x- 1 < 0\) ET \(x+3 < 0\) donc alors
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Donc, pour obtenir cette solution partielle, nous devons intersecter \( x \le 4 \), ou \((-\infty, 4]\) avec \(R_4\).
La solution de pièce correspondante est donc: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Étape 4:
Enfin, nous obtenons l'union des solutions des parties, pour obtenir que la solution de l'inégalité initiale donnée soit
Personne n'a dit que ce serait court, non? Bien. Ce n'est pas vraiment difficile, il suffit d'être systématique et de respecter le plan.
En savoir plus sur les inégalités à valeur absolue
Pourquoi nous inquiétons-nous même de ce genre d'inégalités? Nous nous soucions car ils ont des applications dans la pratique.
Par exemple, en géométrie, les distances sur la ligne réelle doivent être représentées comme une valeur absolue, car elle doit être non négative.
On pourrait avoir une certaine situation géométrique dans laquelle vous devez trouver tous les points de la ligne réelle qui sont au moins à une distance de 2 du point 3. Cette situation peut être décrite avec l'inégalité suivante:
\[| x-3 |\ge 2\]Comprenons l'inégalité ci-dessus. Le point \(x\) est le point où l'on veut satisfaire l'inégalité. La distance entre \(x\) et le point 3 est représentée par \(|x - 3|\).
Ensuite, nous essayons de trouver les points qui sont au moins à une distance de 2 du point 3, alors la distance \(|x - 3|\) doit être au moins 2, ce qui explique le \(|x - 3| \ge 2.\)
Il ne s'agit que d'un type de problèmes d'inégalités de valeur absolue que vous pouvez trouver dans la pratique.
Pouvez-vous trouver des inégalités de valeur absolue sans solution
Tu paries. Ici, vous avez un \(|2x| < |x|\). Il est possible qu'une inégalité soit simplement irréalisable comme le cas de celui que je viens de vous donner.
Que diriez-vous de représenter graphiquement les inégalités de valeur absolue?
Le processus de représentation graphique est essentiellement de pair avec le processus de résolution: vous devez trouver les régions où vous savez exactement si les arguments des valeurs absolues sont positifs ou négatifs, puis les inégalités de valeur absolue deviennent de simples inégalités, qui est graphiquement simplifié . Ensuite, toutes les pièces des régions acquises sont simplement jointes.