Méthode d'intégration de substitution
La méthode d'intégration par substitution ou la méthode d'intégration par substitution est une technique intelligente et intuitive utilisée pour résoudre les intégrales, et elle joue un rôle crucial dans le devoir de résolution des intégrales, avec la intégration par pièces et décomposition des fractions partielles méthode.
L'intégration peut parfois être une opération difficile et nous ne disposons que de quelques outils pour la poursuivre.
Naturellement, le calcul de l'intégrale indéfinie pour certaines fonctions élémentaires de base (comme les polynômes, les puissances, les fonctions trigonométriques élémentaires, etc.) est très simple.
Mais la question est de savoir comment procéder au calcul de l'intégrale indéfinie (ou primitive) pour des fonctions plus complexes ou pour la combinaison algébrique de fonctions.
Es-tu prêt à t'éclater?? Je suis, alors suivez-moi.
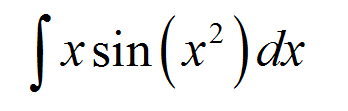
Comment fonctionne la méthode de substitution?
La méthode d'intégration par substitution fonctionne en identifiant un "bloc" qui contient la variable d'intégration, de sorte que le dérivé de ce bloc peut également être trouvé à l'intérieur de l'intégrale. Cette méthode est aussi communément appelée méthode de substitution u.
Si la structure de l'intégrale le permet, ce "bloc" devient en fait une nouvelle variable d'intégration, si tout se passe bien, et l'intégrale se simplifie sérieusement.
Ça marche toujours? Non. Ou dit autrement, vous pouvez toujours faire une substitution, mais cela ne la convertira pas toujours en une intégrale plus facile.
Pourquoi même essayer cette méthode? Eh bien, parce que cela fonctionne souvent. Et c'est généralement la première astuce que vous devriez essayer si vous devez résoudre une intégrale qui n'est pas triviale.
Laissez-nous vous présenter quelques étapes à suivre si vous devez appliquer cette méthode:
ÉTAPE 1:
Examinez la fonction que vous intégrez et recherchez un "bloc", c'est-à-dire une fonction de \(x\) qui apparaît une ou plusieurs fois dans la fonction que vous intégrez.
ÉTAPE 2:
Le "bloc" que vous recherchez doit avoir une propriété très spécifique: le dérivé du bloc doit apparaître une fois et une seule fois dans la fonction en cours d'intégration.
ÉTAPE 3:
Si les étapes précédentes ont réussi, vous pouvez utiliser le "bloc" comme nouvelle variable, et vous pouvez remplacer la variable et le différentiel par la nouvelle variable, et l'intégrale que vous résolvez devient maintenant beaucoup plus simple.
Note technique : Habituellement, j'essaie de garder toutes les explications simples et j'essaie d'éviter les détails techniques. Dans ce cas, je vais devoir donner l'explication technique de la méthode de substitution, pour ne pas laisser les choses trop informelles avec l'idée du "bloc".
Si vous n'aimez pas les aspects techniques, vous pouvez passer à la section suivante, où vous verrez les exemples.
Donc, toute l'idée est d'intégrer une fonction donnée \(f(x)\). Nous devons donc trouver:
\[\int f(x) \, dx\]Dites que la fonction \(f(x)\) n'est pas n'importe quelle fonction et qu'elle a une certaine structure
\[f(x) = g(h(x))h'(x)\]et supposons qu'il existe une fonction \(G(x)\) de sorte que \(G'(x) = g(x)\) (donc \(G\) est la primitive de \(g\)). Ensuite, nous obtenons cela
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Pourquoi donc??? Eh bien, simple: par définition, une primitive est une fonction, de sorte que lorsque vous la différenciez, vous obtenez la fonction que vous intégrez.
Dans ce cas, si vous différenciez \( G(h(x)) \) vous obtenez
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]par la règle de la chaîne ..... et shazam! tu l'as. Je vous ai dit que ce n'était pas si difficile.
Exemples de méthodes de substitution
La meilleure façon d'apprendre à s'intégrer est de pratiquer. Certaines personnes se réjouiront de regarder les preuves, mais la majorité des gens voudront voir les choses en pratique.
Alors, passons aux bases pratiques.
EXEMPLE 1
Trouvez l'intégrale indéfinie suivante:
\[\int x \sin(x^2)\,dx\]RÉPONDRE:
Selon l'étape 1, nous recherchons un bloc, un bloc très spécifique. Si vous regardez l'intégrale, la variable d'intégration est \(x\).
Il y a beaucoup d'essais et d'erreurs, potentiellement, lors de l'utilisation de cette technique. Disons que nous considérons le bloc suivant:
\[u = x^2\]Nous savons que ce bloc est bon car le dérivé de celui-ci est \(u' = 2x\), qui apparaît dans l'intégrale.
Mais alors vous dites "Je vois le \(x\) mais je ne vois pas le 2". Eh bien, il n'est pas nécessaire d'être coincé. On peut faire un truc. Observe ceci
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Qui es-tu, Mandrake le magicien ??? Blagues à part, ce petit truc fonctionne. Ainsi, la substitution de bloc est
\[u = x^2\] \[du = 2x \, dx\](la notation de \(du = 2x \, dx\) est permissive et techniquement incorrecte, mais elle a une base solide, alors soyez indulgents). Faire cette substitution transforme donc l'intégrale en
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Ainsi, une fois que vous êtes passé à la nouvelle variable \(u\), l'intégrale est devenue une intégrale plus facile à résoudre de \(\sin(u)\). Une fois que vous l'avez résolu, vous DEVEZ vous rappeler de revenir à la variable d'origine.
EXEMPLE 2
Maintenant, passons à un exemple un peu plus compliqué. Calculer l'intégrale indéfinie
\[\int e^{x+e^x} \,dx\]en utilisant la méthode de substitution u.
RÉPONDRE:
Qu'est-ce que tu dis ??? Eh bien, ce n'est pas si difficile. Notez que l'intégrale indéfinie peut être réécrite comme:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Alors, maintenant que vous voyez la nouvelle forme de la fonction que vous intégrez, pouvez-vous proposer un "bloc" ou une "substitution en u" ??
N'oubliez pas, n'ayez pas peur de faire des essais et des erreurs. Si quelque chose ne fonctionne pas, essayez autre chose. Et si vous essayiez \(u = e^x\)?
Le dérivé du bloc est \(u' = e^x\), qui se trouve une fois dans la fonction d'origine. De plus:
\[u = e^x\] \[du = e^x \, dx\]On obtient donc:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]En savoir plus sur l'intégration par substitution
Regardons les choses en face: l'intégration peut être difficile. Vraiment dur. Certaines fonctions pas trop compliquées (du moins en apparence) ont donné aux mathématiciens une période terriblement difficile à gérer.
Certaines autres fonctions pas trop compliquées (du moins par les regards) ne sont tout simplement pas résolubles par des méthodes élémentaires.
Alors, vous feriez mieux de croire que l'intégration peut être une épreuve difficile. Vous devez donc vous préparer.
L'un des outils les plus simples et une technique très couramment utilisée est la technique d'intégration par substitution. Oui, il est utilisé car il apparaît fréquemment sur les tests ou les devoirs.
Mais nous avons un peu triché. En réalité, les intégrales qui ont la bonne structure pour être résolues par la technique de substitution sont très spécifiques. La raison pour laquelle vous en voyez de nombreux exemples est que ce sont des fonctions très spécifiques qui sont censées fonctionner pour être intégrées à cette technique.
Mais permettez-moi d'être franc: si vous avez un logiciel conçu pour générer des fonctions aléatoires, et qu'il en génère une pour vous, les chances que vous puissiez utiliser la technique de substitution sont minces.
Pourtant, c'est une petite technique d'intégration puissante qui fonctionne pour une classe très spécifique d'intégrales.
Quelle est la technique de substitution en u?
La 𝘶-substitution avec des intégrales indéfinies est juste un autre nom pour la méthode de substitution. Elle est appelée "𝘶-substitution" car le bloc utilisé est nommé \(u\), donc la nouvelle variable sera u.
Ce n'est certainement pas un bon nom, car le nom que vous choisissez pour votre bloc n'a aucune importance pour le processus de calcul de l'intégrale. Vous pouvez appeler le bloc (et votre nouvelle variable) \(z\) et cela ne ferait aucune différence.