Élimination gaussienne
L'élimination gaussienne est un processus conduit sur des matrices visant à mettre une matrice en forme échelonnée . Avoir une matrice sous une telle forme aide énormément à résoudre très facilement les équations matricielles.
Techniquement, le processus d'élimination gaussienne consiste à trouver une colonne avec un pivot (qui est l'argot de fantaisie pour un élément non nul) qui nous permet d'éliminer tous les éléments sous le pivot.
Ce processus de recherche de pivots et d'élimination nous permet de mettre une matrice en forme d'échelon, et la façon dont le processus se déroule est telle qu'en pivotant, vous ajoutez une nouvelle colonne à la forme d'échelon, et vous ne `` ruinez '' pas l'échelon de vous. ont rattrapé l'étape précédente. Magnifique si vous me demandez.
Le terme «forme échelonnée» qui est obtenu en utilisant l'élimination gaussienne devient clair en regardant la matrice ci-dessus, où les éléments non nuls de la matrice ont cette structure en échelon, comme indiqué par la ligne rouge.
Les mathématiques derrière le pivotement et l'élimination gaussienne
Nous n'allons pas être trop techniques là-dedans, nous allons seulement essayer de comprendre la motivation et les mécanismes de ce type d'élimination.
L'idée est d'obtenir une matrice \(A\), de dimension \(m \times n\) (c'est-à-dire qu'elle a \(m\) lignes et \(n\) colonnes) sous une forme différente qui se prête mieux à la résolution d'équations.
Plus précisément, pour une matrice \(m\times n\) \(A\), et un vecteur \(m\times 1\) \(b\), nous devons trouver un vecteur \(n\times 1\) \(x\) tel que
\[Ax = b\]Vous pensez peut-être, "c'est tellement simple, nous multiplions simplement chaque côté par \(A^{-1}\) à partir de la gauche", donc nous obtenons:
\[x = A^{-1} b \]....Pas si vite! Cela ne fonctionne que lorsque la matrice \(A\) est inversible. Pour commencer, la matrice \(A\) doit être une matrice carrée, puis son déterminant doit être différent de zéro. Mais vous ne pouvez pas multiplier par l'inverse pour les matrices non carrées. Alors, comment faites-vous alors?
Vous devez TRANSFORMER l'équation en une équation plus facile à résoudre.
Plus précisément, les matrices sous forme échelonnée sont des matrices qui conduisent à des équations faciles à résoudre (nous en parlerons plus tard).
Utilisation de matrices élémentaires
Tout d'abord, nous ferons une note cruciale. Si nous avons une solution de l'équation matricielle \(Ax = b\), et \(E\) est une matrice inversible, alors \(x\) est également une solution de \((EA)x = Eb\), et vice versa.
En d'autres termes, les équations matricielles
\[Ax = b\]et
\[(EA)x = Eb\]sont équivalents, pour une matrice inversible \(E\). Qu'entend-on par là les équations sont équivalentes? Nous voulons dire que les équations ont les mêmes solutions.
Donc ce que nous allons faire est de commencer par \(Ax = b\), et en multipliant par des matrices inversibles \(E\), nous allons arriver à une équation matricielle équivalente qui est beaucoup plus facile à résoudre .
Disons que nous sommes capables de trouver une liste de matrices inversibles \(E_1, E_2, ..., E_n\) et nous multiplions (à partir de la gauche) l'équation de la matrice d'origine pour la transformer en une équation équivalente, comme:
\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]où \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) et \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).
Notre objectif est de soigneusement choisir les matrices inversibles \(E_1, E_2, ..., E_n\) pour que \(\tilde A\) soit en échelon.
Pourquoi donc? Parce que si \(\tilde A\) est sous forme échelonnée, résoudre l'équation matricielle \(\tilde A x = \tilde b\) est beaucoup plus facile, et nous savons déjà que \(\tilde A x = \tilde b\) a les mêmes solutions que \(A x = b\)
EXEMPLE 1
Voyons pourquoi la résolution d'une équation matricielle est beaucoup plus facile lorsque vous l'avez sous forme échelonnée. Imaginez d'abord que vous avez la matrice et le vecteur suivants:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]et vous voulez résoudre \(Ax = b\). À quoi ressemblerait le système d'équations? Le système \(Ax = b\) ressemblerait à
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]De quoi ça a l'air? Eh bien, pas si chouette. Vous auriez besoin de commencer à jongler avec les équations. Il existe des approches plus ou moins systématiques pour résoudre ce problème en utilisant des choses comme l'élimination, etc., mais c'est au moins fastidieux.
Maintenant, d'un autre côté, imaginez que vous avez la matrice et le vecteur suivants:
\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]et vous voulez résoudre \(\tilde A x = \tilde b\). Dans ce cas, la matrice \(\tilde A\) est de forme échelonnée. À quoi ressemblerait le système d'équations? Le système \(\tilde A x = \tilde b\) ressemblerait à
\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]À quoi ressemble celui-ci? Eh bien, pas trop minable.
En effet, si nous partons directement de la troisième équation, nous avons ce \(x_3 = -1\) directement. Puis à partir de la deuxième équation, \(x_2 = -1 + x_3 = -1 + (-1) = -2\). Et à partir de la première équation, \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). Donc, sans aucune fuzz, nous avons constaté que:
\[x_1 = -4, \, x_2 = -2, x_3 = -1\]Par conséquent, dans ce cas, le système est résolu de manière triviale.
Pour les systèmes associés à des matrices sous forme échelonnée, il est simple de revenir de la dernière équation à la première équation pour obtenir les solutions.
Comment choisir les bonnes matrices inversibles
Maintenant que nous savons que travailler avec des matrices sous forme échelonnée rend vraiment beaucoup plus facile la résolution des équations matricielles, nous devrions nous demander quelles sont les matrices inversibles \(E_1, E_2, ..., E_n\) qui feront \(\tilde A\) sous forme échelonnée.
Comment fonctionne l'élimination gaussienne?
Fait intéressant, il n'est pas difficile de trouver ces matrices \(E_1, E_2, ..., E_n\), qui seront appelées matrices élémentaires.
Étape 1
: Regardez la première colonne, si elle a une valeur non nulle, ce sera votre pivot. Si la première ligne de la première colonne est différente de zéro, utilisez-la comme pivot. Sinon, recherchez une ligne qui a une valeur différente de zéro et permutez cette ligne et la première ligne.
Donc, vous trouvez un pivot, et potentiellement vous devez faire une permutation de ligne (qui est en fait représentée en multipliant par une certaine matrice inversible)
Étape 2
: Une fois que vous avez un pivot, éliminez tous les éléments de la colonne actuelle, sous le pivot.
Cela se fait en multipliant la ligne du pivot par une certaine constante et en l'ajoutant à une ligne sous le pivot, de sorte que l'élément dans la même colonne que le pivot soit mis à zéro.
Étape 3
: Une fois que tous les éléments sous le pivot ont été remis à zéro en effectuant des opérations de ligne appropriées (qui se trouvent être représentées par l'opération d'une matrice inversible), passez à la colonne suivante, à la ligne suivante, et recherchez un pivot dans la ligne ci-dessous de la rangée du pivot précédent et effectuez la même procédure.
Étape 4
: Répétez jusqu'à ce que vous manquiez de colonnes ou que la matrice soit sous forme d'échelon.
EXEMPLE 2
En utilisant le pivotement et l'élimination gaussienne, résolvez le système suivant:
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]RÉPONDRE:
Tout d'abord, la matrice associée \(A\) et le vecteur \(b\) sont:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]La matrice augmentée \([A|b]\) est
\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]Afin de résoudre le système, nous devons aller à l'élimination gaussienne. Nous choisissons le premier pivot, en commençant par la première colonne. L'élément de la première ligne de la première colonne est 1, qui est différent de zéro, puis il est utilisé comme pivot. Nous utilisons ce pivot (1) pour éliminer tous les éléments en dessous:
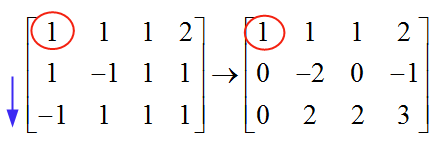
Le mécanisme d'élimination des éléments sous le pivot est simple. Dans ce cas, pour éliminer le "1" qui se trouve sous le pivot, je soustrais les éléments de la rangée 1 aux éléments de la rangée 2. De cette façon, je forme un zéro sous le pivot.
De même, pour éliminer le "-1" qui se trouve dans la rangée 3, j'ajoute les éléments de la rangée 1 aux éléments de la rangée 3. De cette façon, je forme un zéro sous le pivot de la rangée 3.
Nous verrons que ces opérations de ligne sont réalisées en multipliant par une matrice inversible, nous avons donc des systèmes équivalents en faisant cela.
Maintenant, en passant à la ligne suivante, colonne suivante, nous trouvons un "-2", qui est différent de zéro, et par conséquent, il est utilisé comme notre pivot. Pour éliminer la valeur sous ce pivot, nous ajoutons à la ligne 3 les valeurs de la ligne 2:
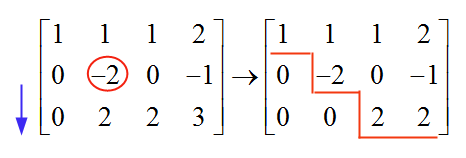
et maintenant nous nous arrêtons, car la matrice résultante est déjà sous forme d'échelon. Maintenant, nous faisons marche arrière pour résoudre le système:
\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]En savoir plus sur l'élimination gaussienne
Le pivotement et l'utilisation de l'élimination de pivot sont la pierre angulaire de la résolution de systèmes linéaires. Mais cela va plus loin. Si nous ne nous intéressions qu'aux systèmes linéaires, nous utiliserions Règle de Cramer , qui fonctionne très bien pour résolution de systèmes .
L'élimination gaussienne a l'avantage de donner un moyen systématique de mettre les matrices en échelon de rangées, ce qui conduit à son tour à l'obtention rapide de certaines décompositions matricielles (LU, LDU, etc.), voire au calcul de l'inverse de la matrice .
Matrices élémentaires de permutation
Il n'y a pas de règles générales pour factoriser les expressions générales. Nous devons jouer à l'oreille et essayer d'exploiter la structure de l'expression. Parfois, nous pouvons prendre en compte, parfois nous ne pouvons pas. Tout dépend de l'expression. La seule règle générale est d'essayer de grouper et d'essayer de trouver des facteurs communs afin de grouper et de simplifier davantage.
Matrices élémentaires d'opérations sur les lignes
La clé de la méthode pivot pour trouver des solutions est que les permutations et les opérations de ligne sont des matrices inversibles, de sorte que le système que nous transformons à chaque étape est équivalent au système d'origine.
En effet, tant la permutation des lignes que les opérations de lignes sont représentées par des matrices inversibles. Considérons la matrice \(E_{ij}\), qui est obtenue en prenant la matrice d'identité \(I\) et en permutant ses lignes \(i\) et \(j\).
La multiplication de la matrice \(E_{ij}\) en n'importe quelle matrice \(A\) à partir de la gauche est d'obtenir les lignes \(i\) et \(j\) de \(A\) permutées.
Considérons maintenant la matrice \(E_{ij}^{\lambda}\), pour \(i < j\), qui correspond à la matrice d'identité pour toutes les lignes, sauf pour la ligne \(i\), où la valeur du i e la colonne est \(\lambda\) au lieu de 0.
Qu'en est-il des opérations avec des colonnes?
Parfois, nous devons permuter les colonnes pour trouver un pivot. Dans ce cas, nous devons multiplier la matrice \(E_{ij}\) à partir de la DROITE, et le résultat sera d'obtenir les colonnes \(i\) et \(j\) de \(A\) permutées.