Calculatrice de fractions
Instructions : Utilisez cette calculatrice de fraction pour calculer n'importe quelle opération ou calcul de fraction que vous fournissez, en montrant toutes les étapes. Veuillez saisir le calcul de fraction que vous souhaitez effectuer dans le champ de formulaire ci-dessous.
En savoir plus sur cette calculatrice de fractions
Cette calculatrice vous permettra l'addition de fractions , multiplier des fractions , diviser des fractions etc., et toute opération de fraction valide, en montrant toutes les étapes. Vous devez fournir une expression valide impliquant des fractions. Il peut s'agir d'une expression simple comme "1/2 + 1/3" ou d'une expression plus complexe comme "(1/3+1/4)(1/5+1/6)".
Une fois que vous avez fourni une expression valide impliquant une fraction, tout ce que vous avez à faire est de cliquer sur le bouton "Calculer", et toutes les étapes des calculs vous seront fournies.
L'algèbre des fractions implique la conversion des fractions, comme l'utilisation du dénominateur commun, et l'utilisation des règles arithmétiques de base. Dans l'ensemble, le processus de calcul peut être laborieux, bien qu'il puisse être effectué de manière systématique, sans grand problème.
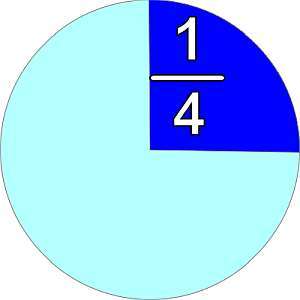
Comment calculer les fractions
Pour calculer des fractions, vous utiliserez une méthodologie très simple et directe, qui dépendra de l'opération (addition, soustraction, multiplication ou division) que vous souhaitez effectuer. Chaque opération a sa propre logique.
En termes simples, les additions et les soustractions nécessitent de trouver une dénominateur commun alors que la multiplication et la division opèrent directement sur les numérateurs et les dénominateurs. Plus de détails à ce sujet dans les paragraphes ci-dessous.
Comment additionner des fractions ?
L'addition de fractions est l'une des compétences les plus cruciales et les plus fondamentales que vous utiliserez pour calculer des opérations sur des fractions. En général, vous devez commencer par trouver un dénominateur commun, mais souvent, vous utiliserez la formule suivante pour l'addition de fractions :
\[\displaystyle \frac{a}{b} + \frac{c}{d} = \displaystyle \frac{ad + cb}{bd} \]Quelles sont les étapes de l'addition de fractions ?
- Étape 1 : Identifiez le numérateur et le dénominateur de la première et de la deuxième fraction
- Étape 2 : Supposons que a et b soient le numérateur et le dénominateur de la première fraction, et que c et d soient le numérateur et le dénominateur de la deuxième fraction
- Étape 3 : Utilisez la formule d'addition : La fraction résultante a ad + cb comme numérateur et bd comme dénominateur
La soustraction de fractions est simplement dérivée de la somme des fractions : Pour soustraire deux fractions, il suffit de multiplier la seconde par -1, puis de l'ajouter à la première .
Comment multiplier des fractions ?
La deuxième pierre angulaire pour effectuer des calculs généraux de fractions est la multiplication de fractions. Dans ce cas, il n'est pas nécessaire de trouver un dénominateur commun, vous allez simplement multiplier les numérateurs et les dénominateurs ensemble :
\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]Quelles sont les étapes de la multiplication des fractions ?
- Étape 1 : Identifiez le numérateur et le dénominateur de la première et de la deuxième fraction
- Étape 2 : Supposons que a et b soient le numérateur et le dénominateur de la première fraction, et que c et d soient le numérateur et le dénominateur de la deuxième fraction
- Étape 3 : Utilisez la formule d'addition : La fraction résultante a ad + cb comme numérateur et bd comme dénominateur
Comme pour l'addition et la soustraction, la division de fractions est simplement dérivée de la multiplication de fractions : Pour diviser deux fractions, il suffit de multiplier la première par la seconde fraction inverse du second (la fraction inverse est obtenue en échangeant le numérateur par le dénominateur dans la fraction).
De la décimale à la fraction
You can convertir n'importe quelle décimale en fraction à l'aide d'une astuce simple. Certaines décimales seront plus faciles à convertir, notamment celles qui ont un nombre fini de décimales. Les décimales périodiques peuvent également être converties. Voici la marche à suivre :
- Étape 1 : Identifiez le type de nombre avec lequel vous travaillez et déterminez s'il comporte des chiffres décimaux ou non. Si c'est le cas, évaluez le nombre de décimales qu'il contient
- Étape 2 : Si D ne comporte pas de décimales, la conversion en fraction est directe, comme nous le savons \(D = \frac{D}{1}\)
- Étape 3 : Si D a un nombre fini de chiffres décimaux, disons qu'il a k décimales. Dans ce cas, vous multipliez D par \(10^k\) pour éliminer les décimales, puis vous trouvez que \(D = \frac{D \times 10^k}{10^k}\), et vous réduisez la fraction si nécessaire.
- Étape 4 : Si D a un nombre infini de décimales, il est donc périodique : Multipliez le nombre par une puissance de 10 qui, en faisant 10D - D, élimine la périodicité, et vous obtenez alors que 9D est une décimale finie, que vous traitez à l'aide de l'étape 3.
Par exemple, vous pouvez demander ce que représente 1,214285714 en tant que fraction, et nous remarquons que D = 1,214285714 a 9 chiffres après la virgule. Nous observons donc que
\[D = 1.214285714 = \frac{1.214285714 \times 10^9}{10^9} = \frac{1,214,285,714}{1,000,000,000} = \frac{607,142,857}{500,000,000} \]Pour un nombre périodique, disons que vous avez D = 2,349999999.... La partie périodique commence à la troisième position décimale, nous multiplions donc D par 100. Nous obtenons 100D = 234.999999....
Maintenant, nous soustrayons D de 100D et nous obtenons \(100D - D = 234.999999.... - 2.349999 = 232.65\), ce qui implique que \(99D = 2.3265\), qui peut être traité comme suit :
\[99D = 232.65 \Rightarrow 9900D = 23265 \Rightarrow D = \frac{23265}{9900} = \frac{47}{20} \]Relation entre les pourcentages et les fractions
Comme vous vous en doutez probablement, les pourcentages et les fractions sont étroitement liés. Par exemple, un pourcentage de 80 % correspond à un simple 0,80, qui est une décimale, et les étapes ci-dessus permettent de le convertir directement en fraction.
Puis, comme les décimales et les fractions sont si intimement liées, un Calculateur De Pourcentage et un Calculatrice de fractions sont également étroitement liés.
Pourquoi s'intéresser au calcul des fractions ?
Les fractions sont l'une des pierres angulaires de l'algèbre et de tout système général expression algébrique pour calculer . Les fractions sont des opérandes simples, mais qui peuvent être composées en termes plus compliqués à l'aide d'opérations comme la somme, la multiplication, etc., puis à l'aide de fonctions, nous pouvons construire des expressions encore plus avancées.
Le centre de toute calculatrice algébrique commence par la puissance des nombres de base des fractions.
Exemple : calcul de la somme de fractions
Calculez ce qui suit : \(\frac{1}{3} + \frac{5}{4} - \frac{5}{6}\)
Solution :
Nous devons calculer et simplifier l'expression suivante : \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\).
On obtient le calcul suivant :
qui conclut le calcul.
Exemple : un autre calcul de fraction
Calculer \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).
Solution :
Nous devons calculer et simplifier l'expression suivante : \(\displaystyle \left(\frac{2}{3}\cdot\frac{6}{5}\right)+\frac{2}{5}\).
On obtient le calcul suivant :
qui conclut le calcul.
Autres calculatrices de fractions utiles
Les calculs de fractions sont cruciaux en algèbre. D'autres opérations utiles sont simplifier une fraction en réduisant à ses conditions les plus basses. Vous pouvez également convertir une fraction en pourcentage ou fraction en décimal car ils ont un lien intime.
Aussi, vous pourriez être intéressé par un calculatrice de fractions mixtes selon le contexte d'apprentissage. Dans les contextes plus élémentaires, les nombres mixtes sont traités comme des entités importantes, tandis que dans les contextes plus avancés, les nombres mixtes sont simplement présentés dans leur notation fractionnaire...




