Calculateur de pente perpendiculaire
Instructions: Utilisez cet outil graphique pour tracer la recherche, étape par étape, de la pente d'une ligne perpendiculaire à une ligne qui a une pente donnée. Veuillez fournir la pente de votre ligne (toute expression numérique valide).
En savoir plus sur ce calculateur de pente perpendiculaire.
Souvent, nous devons traiter des lignes et d'autres lignes qui leur sont perpendiculaires. La perpendicularité est liée au fait d'avoir un 90 O angle entre les lignes.
Mais la question est, comment pouvons-nous relier cela perpendicularité de deux droites avec les pentes des deux droites ?
La réponse est simple : deux droites de pentes \(m_1\) et \(m_2\) sont perpendiculaires si et seulement si
\[m_1 \cdot m_2 = -1\]
Comment calculer la pente perpendiculaire ?
La réponse est là. Si vous connaissez \(m_1\), alors tout ce que vous avez à faire est de résoudre la pente de la droite perpendiculaire, \(m_2\), nous obtenons donc ce qui suit formule de la pente perpendiculaire :
\[\displaystyle m_2 = -\frac{1}{m_1}\]qui est la formule de la pente perpendiculaire de la pente de la ligne .
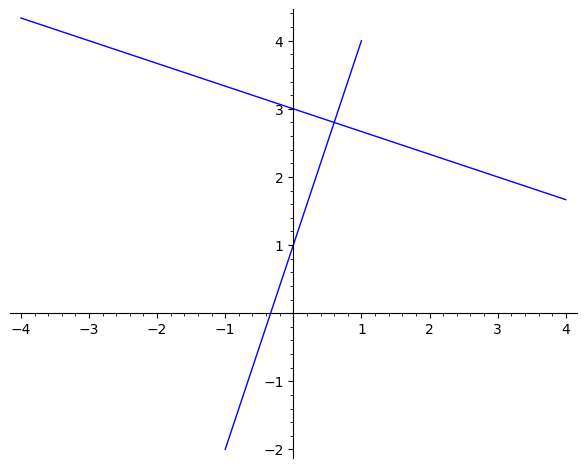
Comment calcule-t-on la pente perpendiculaire si on a l'équation d'une droite ?
Dans ce cas, la première chose à faire est de convertir l'équation en forme pente-ordonnée à l'origine . Une fois que vous connaissez la pente, vous pourrez utiliser la formule présentée ci-dessus.
En fin de compte, une fois que vous avez la pente de la ligne perpendiculaire, en sachant qu'un point de cette ligne perpendiculaire passe par, vous pouvez réellement calculer l'équation de la droite perpendiculaire .
Exemple : calcul de la pente d'une droite perpendiculaire
Considérez la droite d'équation \(x + 3y = 2)\). Trouver la pente de la droite perpendiculaire à la droite donnée.
Solution: L'équation peut être réécrite comme suit : \[3y = -x + 2\] \[\Rightarrow y = \displaystyle -\frac{1}{3} x + \frac{2}{3}\] Par conséquent, la pente donnée de la ligne fournie est \(m = \displaystyle -\frac{ 1}{ 3}\), et nous devons calculer la pente perpendiculaire.
La formule nécessaire pour calculer la pente perpendiculaire, \(m_{\perp}\), est :
\[m_{\perp} = \displaystyle -\frac{1}{m}\]En insérant la valeur de \(m = -\frac{ 1}{ 3}\) dans la formule, on trouve que la pente perpendiculaire est
\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{-\frac{ 1}{ 3}} = 3\]Par conséquent, nous concluons que la pente perpendiculaire est \(m_{\perp} = 3 \)