Calculadora de fórmula del punto medio

Esta calculadora te permitirá encontrar el punto medio entre dos puntos. Todo lo que tiene que hacer es proporcionar las coordenadas de los dos puntos y luego hacer clic en "Calcular" para que se muestren todos los pasos.

En primer lugar, debemos recordar que el distancia entre dos puntos en el plano euclidiano se basa en el concepto de los principios geométricos básicos que permiten utilizar el teorema de Pitágoras.

¿cómo se calcula el punto medio?

Conceptualmente hablando, el punto medio es el punto que está Medio camino entre los dos puntos. Esta idea de término medio está en consonancia con los teoremas geométricos de proporcionalidad.

El punto medio es un par ordenado que se encuentra a medio camino entre dos puntos dados. Eso es lo primero que debes saber: algunas personas piensan erróneamente que una cantidad es el punto medio y, en realidad, lo que se busca obtener es un par ordenado.

El punto medio de los puntos \((x_1, y_1)\) y \((x_2, y_2)\) dados viene dado por la siguiente fórmula:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]

Explicación de la fórmula del punto medio.

Definición De Fórmula: La fórmula del punto medio anterior está estrechamente relacionada con la fórmula de distancia . De hecho, lo que hace la fórmula anterior es muy simple: toma el promedio de las dos coordenadas correspondientes.

Es decir, la primera coordenada del punto medio es el promedio de las primeras coordenadas de los dos puntos dados, y la segunda coordenada del punto medio es el promedio de las segundas coordenadas de los dos puntos dados. ¿Cómo utilizar la fórmula anterior? Consulte los ejemplos a continuación.

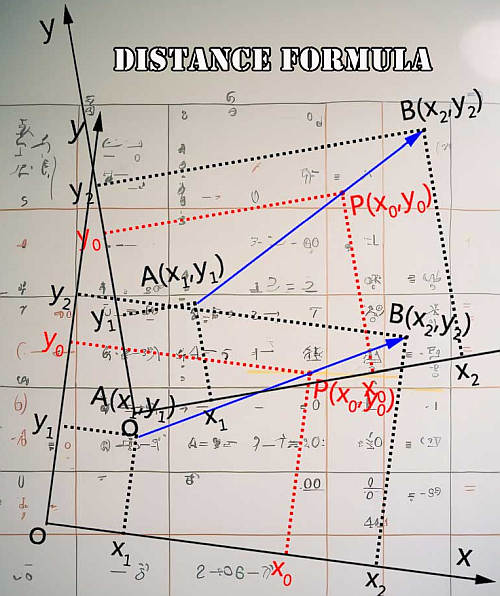
¿para qué uso la fórmula del punto medio?

La idea de punto medio nos resulta tan familiar porque está estrechamente asociada a la idea de "a mitad de camino" de un punto a otro. Este tipo de situaciones son muy habituales en la vida real, donde nos puede interesar dividir algo, por ejemplo.

Naturalmente, el proceso de dividir algo no tiene por qué implicar necesariamente un punto medio, pero normalmente cuando se hace una división igual, sí lo será.

Entonces, la fórmula del punto medio es tan útil en parte porque es una forma de usando la fórmula de la distancia en un caso muy especial, donde el punto que estamos encontrando está a la misma distancia de ambos puntos dados.

Ejemplos de fórmulas del punto medio

Supongamos que tenemos dos puntos \((1, 3)\) y \((4, 8)\), entonces la fórmula del punto medio se calcula de la siguiente manera:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{1 + 4}{2}, \frac{3+ 8}{2} \right) = \left( \frac{5}{2}, \frac{11}{2} \right) \]

A veces dejas la respuesta como una fracción, o a veces se te indica que calcules la respuesta con decimales, en cuyo caso el punto medio sería (2,5, 5,5) en el ejemplo anterior.

Más ejemplos de punto medio

¿Cómo lidiar con la fórmula del punto medio con fracciones? Es el mismo procedimiento. Supongamos que tenemos dos puntos \((\frac{1}{2}, \frac{1}{4})\) y \((\frac{3}{5}, \frac{3}{4})\), entonces el punto medio se calcula como:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = \left( \frac{1/2 + 3/5}{2}, \frac{1/4+ 3/4}{2} \right) = \left( \frac{11/10}{2}, \frac{1}{2} \right) = \left( \frac{11}{20}, \frac{1}{2} \right) \]

¿tiene esto algo que ver con pitágoras?

Casi todo tiene que ver con Pitágoras . El punto medio de la hipotenusa se proyectará al punto medio de los catetos de un triángulo rectángulo. Además, puedes tomar los dos puntos y calcular la distancia entre ellos , usando la fórmula pitagórica.