Solvers Álgebra

Calculadora de decimales a fracciones

Instrucciones: Utilice esta calculadora para convertir un decimal dado que usted proporciona a fracción, mostrando todos los pasos. Por favor, introduzca un número decimal (por ejemplo, un número como '3.4673' o un número como '.345279') en el siguiente formulario:

Acerca de esta calculadora de decimales a fracciones

¿Qué es un decimal? Un decimal se refiere a una forma de expresar los números utilizando el número de diez como base, así como las potencias de diez y las décimas.

En palabras sencillas, los decimales son números tal y como los conoces, esto, tienes una secuencia de dígitos (números entre 0 y 9), seguidos posiblemente de décimas, representadas por un punto "." y una secuencia de dígitos

Ejemplo de dígito: Por ejemplo, 45,34556 y 0,5678 son dígitos. Los dígitos que sólo tienen un "0" a la izquierda de la "." suelen escribirse como .4534, en aras de la brevedad.

¿Cómo se convierte un decimal en una fracción?

La estrategia es sencilla: hay que intentar "eliminar" los decimales (los dígitos a la derecha de la ".") multiplicando el número por una potencia de 10.

Una vez que lo hagas, toma nota de la potencia de 10 que utilizaste para lograrlo, porque luego la utilizarás para convertir el número dado en un decimal.

Por ejemplo, si se tiene el número 2,34, hay que multiplicar por 100 para "eliminar" los decimales, por lo que se obtiene $2.34 \cdot 100 = 234$. En este caso, el número después de "eliminar" los decimales es $N = 234$ y la potencia de 10 utilizada es $10^2 = 100$.

Fórmula de decimales a fracciones

Paso 1 : Sea D un número con cifras decimales. Se multiplica $D$ por una potencia de 10, para que no haya más dígitos a la derecha de la ".", o como dirían algunos, para que no haya decimales en el número.

Paso 2 : Del paso anterior, tienes la potencia de 10 que usaste para "eliminar" los decimales, di que ese número es $10^k$, y di que $N$ es el resultado después de "eliminar los decimales".

Paso 3 : La fórmula para expresar el número dado en una fracción es

\[ D = \displaystyle\frac{N}{10^k}\]

y, posiblemente, quiera reducir la fracción a la derecha hasta su mínima expresión.

Tabla de Decimal a Fracción

Existen tablas clásicas que le proporcionan una visión clara de la equivalencia de las fracciones más utilizadas y sus conversiones decimales.

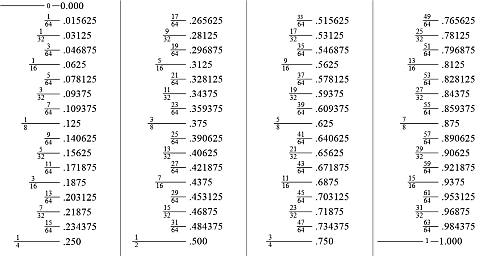
Ventajas y desventajas de utilizar una tabla frente a la fórmula para convertir decimales en fracción

El uso de un gráfico es directo: basta con mirar el gráfico y obtener la conversión decimal-fracción inmediatamente
El problema con el gráfico es que el decimal o la fracción precisa que se busca no está ahí
Utilizando la fórmula de conversión, te aseguras de que puedes convertir CUALQUIER número, pero en realidad tienes que trabajar en el cálculo.

Calculadoras sobre fracciones y porcentajes

Naturalmente, como probablemente te hayas dado cuenta ahora, las fracciones, los decimales y los porcentajes están estrechamente relacionados. Y, a menudo, no son más que formatos diferentes para representar la misma información de una manera más conveniente para un contexto determinado.

Por ejemplo, el uso de una calculadora de porcentaje a fracción hace un trabajo similar al de esta calculadora de decimales a fracción, con la diferencia de que primero tendrás que convertir el decimal a porcentaje.

Naturalmente, es posible que usted se enfrente a la situación inversa. Tal vez quiera convertir un fracción a un decimal , que es simplemente el algoritmo común de la Aritmética de la división. Observe que la conversión de una fracción en un decimal puede conducir a un número decimal finito, o potencialmente a un decimal repetido.

Por ejemplo, la fracción $\displaystyle \frac{3}{5}$ corresponde simplemente a 0,6 (un decimal simple y finito), pero la fracción $\displaystyle \frac{1}{3}$ corresponde al decimal repetitivo 0,33333.....

$decimal a fracción$

Ejemplo: Conversión de Decimal a Fracción

Pregunta : Calcula el número 3,4563 como fracción.

Solución:

Has proporcionado el siguiente decimal $D = \displaystyle 3.4563$, y el objetivo es convertirlo en una fracción.

Paso 1: Tenemos que multiplicar $D = 3.4563$ por una potencia de 10, para que la expresión resultante no tenga valores decimales, a la derecha del signo '.'.

Paso 2: Esto se hace simplemente contando el número de dígitos a la derecha del punto '.'. Para el número proporcionado, tenemos $k = 4$ dígitos a la derecha del punto.

Por lo tanto, la potencia de 10 necesaria es $10^{k} = 10^{4} = 10000$. Por lo tanto, encontramos que

Paso 3: Por lo tanto, encontramos que

\[ N = D \times 10^k = 3.4563 \times 10^{4} \] \[ = 3.4563 \times 10000= 34563 \]

Entonces, dividiendo ambos lados por $10000$, obtenemos

\[ 3.4563 = \displaystyle \frac{34563}{10000} \]

y como la fracción encontrada ya está simplificada, se concluye que la fracción más simple equivalente a $3.4563$ es $3.4563$.

Por lo tanto, la expresión del decimal como fracción en sus términos más simples es $\displaystyle 3.4563 = \frac{ 34563}{ 10000}$, con lo que se concluye el cálculo.