Mehr über diese Fläche und das Volumen eines Pyramidenrechners

Dieser Rechner behandelt quadratische Pyramiden (solche Pyramiden mit quadratischer Basis), für die Sie die Seite $l$ der Basis und die entsprechende Höhe $h$ angeben müssen. Eine quadratische Pyramide sieht aus wie:

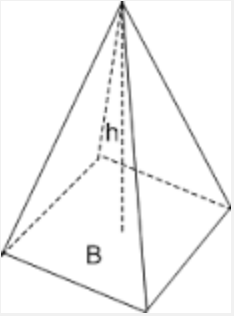
Wie berechnet man die Fläche und das Volumen einer Pyramide?

Um die Oberfläche und das Volumen der quadratischen Pyramide mit der Seite $l$ und der Höhe $h$ zu berechnen, verwenden wir die folgenden Formeln:

$$\text{Area} = l^2 + 2l\sqrt{\frac{l^2}{4} + h^2}$$ $$\text{Volume} = \frac{l^2 h}{3}$$

Aus rechnerischer Sicht ist es recht einfach, die Oberfläche und das Volumen einer quadratischen Pyramide zu berechnen, indem einfach die Seite $l$ und die Höhe $h$ in die obigen Formeln eingefügt werden. Wenn zum Beispiel die Seite $l = 3$ und die Höhe $h = 4$ ist, berechnen wir

$$\text{Area} = l^2 + 2l\sqrt{\frac{l^2}{4} + h^2} = 3^2 + 2\cdot 3\sqrt{\frac{3^2}{4} + 4^2} = 34.632$$ $$\text{Volume} = \frac{l^2 h}{3} = \frac{3^2\cdot 4}{3} = 12$$

Damit ist die Berechnung abgeschlossen.

Andere geometrische Taschenrechner

Unsere Website bietet eine Reihe von geometrischen Taschenrechnern, einschließlich dieser Kugelflächen- und Volumenrechner , unter vielen anderen.