Restplot Grapher
Anleitung: Verwenden Sie diesen Residual Plot Grapher, um ein Residuendiagramm für den Wert zu erstellen, der mit einer linearen Regressionsanalyse auf der Grundlage der von Ihnen bereitgestellten Probendaten erhalten wurde. Bitte geben Sie die Daten für die unabhängige Variable \((X)\) und die abhängige Variable (\(Y\)) in das folgende Formular ein:
Über diesen Restplot Grapher
Eine der Hauptanforderungen für die Gültigkeit der Ergebnisse und Vorhersagen einer Regressionsanalyse ist die Erfüllung der linearen Regressionsannahmen. Die Annahmen von Unabhängigkeit, Normalität und Homoskedastizität von Fehlern sind entscheidend für zuverlässige Regressionsergebnisse
Die Verwendung von Plots basierend auf Residuen ist entscheidend, um schnell beurteilen zu können, ob die Annahmen nicht erfüllt sind oder nicht und ob eine Korrektur erforderlich ist.
Sobald wir die Regressionskoeffizienten geschätzt haben, die dem y-Achsenabschnitt und der Steigung \(\hat \beta_0\) und \(\hat \beta_1\) entsprechen, können wir mit der Berechnung der vorhergesagten Werte fortfahren.
Wie berechnet man Regressionsrestwerte?
Die Berechnung ist einfach. Der erste Schritt besteht in der Berechnung der linearen Regressionskoeffizienten, die auf folgende Weise zur Berechnung der vorhergesagten Werte verwendet werden:
\[ \hat y = \hat \beta_0 + \hat \beta_1 x \]Sobald die vorhergesagten Werte \(\hat y\) berechnet sind, können wir die Residuen wie folgt berechnen:
\[\text{Residual} = y - \hat y\]Was zeigt Ihnen ein Restplot?
Restdiagramme werden verwendet, um lineare Regressionsannahmen zu verifizieren. Es ist eine visuelle Möglichkeit, schnell zu beurteilen, ob die Annahmen ernsthaft verletzt werden oder nicht. Für eine präzisere Beurteilung der Erfüllung der linearen Regressionsannahmen gibt es für jede Annahme einen spezifischen statistischen Test.
Die verschiedenen Arten von Residuendiagrammen sind: Residuen gegenüber Beobachtungszahl (von diesem Rechner bereitgestellt), anhand derer die Hypothese der Fehlerunabhängigkeit bewertet wird. Wir haben auch das Normalitätsdiagramm der Residuen (das zur Bewertung der Normalität von Fehlern verwendet wird) und das Diagramm der Residuen gegenüber dem vorhergesagten Wert, das zur Bewertung der Annahme der Homoskedastizität des Fehlers verwendet wird.
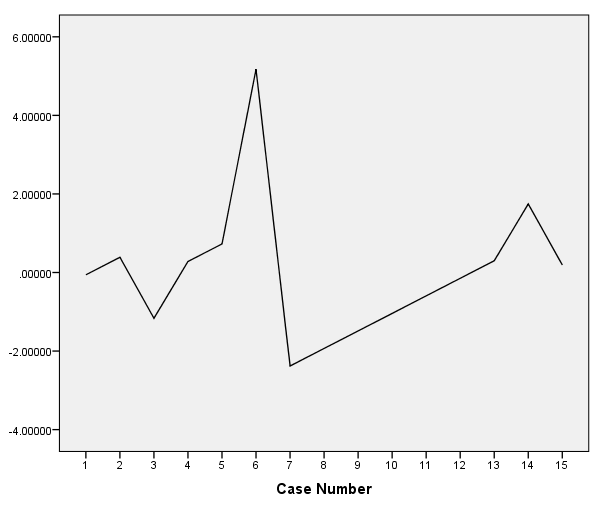
Wie stellen Sie Residuen aus einem linearen Regressionsmodell grafisch dar?
Es gibt verschiedene Arten von Plots mit Residuen. Dieser Rechner zeigt Ihnen die Berechnung der Residuen und ein Diagramm der Residuen gegenüber der Beobachtungszahl.
Mit diesem Residuen-Plot-Maker können Sie beurteilen, ob die Residuen zeitlich zufällig erscheinen (unabhängig voneinander) oder ob es zeitlich ein Muster gibt (was darauf hindeutet, dass die Residuen nicht unabhängig sind, und a Regressionsannahme würde verletzt).
Wenn Sie nur Regressionsergebnisse berechnen müssen, können Sie dies verwenden lineares Regressionsmodell Rechner , um die geschätzten Regressionskoeffizienten basierend auf den bereitgestellten Probendaten zu erhalten.
