Reihenfolge der Operationen
Die Reihenfolge der Operationen besteht aus einer Reihe von Konventionen zum Ausführen von Operationen für einen algebraischen Ausdruck (z. B. \(2+3\times 4\)), wenn Unklarheiten hinsichtlich der Durchführung der Operation bestehen können, da mehr als eine Operation vorhanden ist.
Die Reihenfolge der Operationen bestimmt die Rangfolge der Operationen bei der Auswertung eines algebraischen Ausdrucks, der herkömmlicherweise dem PEMDAS-Kriterium folgt.
Im Beispiel des algebraischen Ausdrucks \(2+3\times 4\) gibt es eine Addition (\(+\)) und auch eine Multiplikation (\(\times\)). Welches mache ich zuerst? Denken Sie daran, dass Operationen zwischen zwei Operanden gleichzeitig stattfinden. Wenn ich mehr als zwei Operanden habe, muss ich zuerst zwei davon operieren und so weiter. Aber welches zuerst?
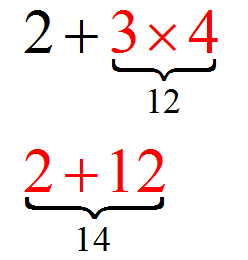
Technisch gesehen sollten wir überall Klammern verwenden, um genau zu bestimmen, welche Paare zuerst operiert werden und wie die Operation nacheinander durchgeführt wird. Zum Beispiel könnten wir im Ausdruck \( 2 + 3\times 4\) \( (2 + 3)\times 4\) schreiben oder \( 2 + (3\times 4)\).
Warum müssen wir also über eine Konvention für den Vorrang von Operationen nachdenken, wenn dies perfekt mit Klammern einhergehen kann, um Unklarheiten zu vermeiden? Die Antwort ist Einfachheit.
Was würde zum Beispiel mit so etwas wie \( 2 + 3 \times 4 - 3/2\) passieren?
Wenn wir gezwungen sind, Klammern anzugeben, um ALLE Operationen anzugeben, müssten wir \( (2 + 3) \times (4 - 3/2)\) oder \( (2 + (3 \times 4)) - (3/2)\) oder \( 2 + ((3 \times 4) - (3/2))\) und weiter und weiter und weiter schreiben. Es wird schwer.
Sie raten also richtig. Wenn Sie mehr Operanden in einem komplexeren Ausdruck erhalten, würde es sehr mühsam sein, einen Ausdruck zu schreiben, wenn Sie alle auszuführenden Operationen in Klammern angeben müssen.
Im Allgemeinen erspart uns die Erstellung einer Konvention zur Vorrangstellung von Operationen viel Aufwand, um eindeutige Ausdrücke zu schreiben.
Die PEMDAS-Konvention
Das PEMDAS ist ein mnemonisches Akronym, mit dem Sie sich an die Rangfolge der Operationen erinnern können, die als Standardkonvention verwendet werden.
P = Klammern zuerst
E = Exponenten weiter
MD = Multiplikationen und Divisionen als nächstes
AS = Additionen und Subtraktionen am Ende
Wenn wir diese Konvention für die Reihenfolge der Operationen verwenden, sparen wir viel Zeit, indem wir keine überflüssigen Klammern schreiben müssen, und nur diese müssen die Standardmethode überschreiben, mit der PEMDAS bei Bedarf die Reihenfolge der Berechnung ausführt.
.BEISPIEL 1
Bewerten Sie \(3+(3\times 12)\). Könnten Sie diesen Ausdruck einfacher geschrieben haben?
.ANTWORTEN:
Laut PEMDAS führen wir die Operationen zuerst in Klammern durch:
\[3+(3\times 12) = 3 + 36 = 39\]Dieser Ausdruck hätte einfacher wie \(3+3\times 12\) ohne die Klammer geschrieben werden können, da Sie in diesem Fall laut PEMDAS die Multiplikation vor der Summe berechnen würden.
BEISPIEL 2
Berechnen Sie \((18\div 6\times 5) - 14 \div 7 \).
ANTWORTEN:
Unter Verwendung der PEMDAS-Konvention machen wir die Klammern und dann Multiplikationen sind Divisionen und nur am Ende mache ich die Subtraktion. Wir bekommen:
\[(18\div 6\times 5) - 14 \div 7 \] \[= (3 \times 5) - 14 \div 7 \] \[= 15 - 14 \div 7 \] \[= 15 - 2 \] \[= 15 - 13 \]Wir machen es auf dem langen Weg, entschädigen wir jeden kleinen Schritt zeigen. Es ist in Ordnung, wenn Sie es schneller machen, ohne so viele Details zu erhalten, obwohl es mit PEMDAS am besten ist, langsam zu fahren, um keinen Fehler zu machen.
Weitere Informationen zur Verwaltung der Operationen
Eine Standardregel für die Rangfolge von Operationen zu haben, verloren unser Leben, wenn es darum geht, einen algebraischen Ausdruck zu schreiben.
Sie müssen sich darum kümmern, alle sich um Klammern zu kümmern, um sich zu kümmern, um sich zu kümmern, um sich zu kümmern, um sich zu kümmern, um sich zu kümmern, um sich zu kümmern, um sich zu kümmern.
Wenn Sie im Beispiel \(2+3\times 4\) zuerst \(3\) und \(4\)
Wenn Sie allein haben
Auch welche Operation heißt, welche gehören werden?
Wenn Sie diese Lektion beachtungsberechtigt sind, werden Sie gehört, dass die Steuerungen, Pensionen, E (Exponenten), MD (Multiplikationen und Divisionen) und AS (Addition und Subtraktion) )).
Warum ist das die verschiedenen der Operationen in dieser Verantwortung?
PEMDAS ist nur eine Konvention. Aber es ist eine Konvention, die wird wird, und es ist eine Konvention, die nach anderen arithmetischen letzten Sinn macht. Daher wird PEMDAS als Standard verwendet, obwohl es sich um eine willkürliche Konvention handelt.
Es ist wichtig, eine lustige Kunst zu haben, sich die PEMDAS-Konvention zu erinnern, das Auswendiglernen des letzten sehr eingängigen Satzes: "Bitte kaufen Sie meine liebe Tante Sally ".
Ist das MDAS gehört wie PEMDAS?
Im gehört ja. MDAS steht für Multiplikation - Division - Addition - Subtraktion im Sinne der Rangfolge von Operationen ohne Klammern. Es wird implizit verursacht, dass Klammern vorübergehend operiert werden.
Macht es einen Unterschied für die Kontrolle der Operationen mit Klammern?
Nein, tut es nicht. Die Klammer in Klammern finden genau die gleichen Rolle wie die reguläre Klammer. Wird verwendet, um das Muster zu ändern verschachtelter Klammern zu brechen, nur um das Lesen zu gehört.
Zum Beispiel gehört Sie so etwas wie \((((3+4)\times 4) - 3) \div 1 \) haben. Die drei verschachtelten Klammern auf der linken Seite sind schwer zu lesen, die sie unterschiedlich zu lesen sind, wenn wir wissen \(([(3+4)\times 4] - 3) \div 1 \) schreiben. Regelweise Klammern und Klammern sind auch gleich, aber es ist eine gute Praxis, sie bei verschachtelten Klammern zu gehören.
Schauen Sie sich unsere algebraischer Ausdrucksrechner , die PEMDAS verwendet, um jeden Ausdruck Ausdruck zu bedienen. Stellen Sie sicher, dass Sie PEMDAS verwenden, oder verwenden Sie Klammern, wenn Sie Zweifel an der korrekten Verwaltung von Operationen haben.
