Berechnung der mittelpunktsformel

Dieser Rechner ermöglicht es Ihnen, den Mittelpunkt zwischen zwei Punkten zu finden. Sie müssen nur die Koordinaten der beiden Punkte angeben und dann auf "Berechnen" klicken, um alle Schritte angezeigt zu bekommen.

Zunächst einmal ist daran zu erinnern, dass die abstand zwischen zwei Punkten in der euklidischen Ebene beruht auf dem Konzept der geometrischen Grundprinzipien, die die Anwendung des Satzes von Pythagoras ermöglichen.

Wie berechnet man den mittelpunkt?

Konzeptionell gesehen ist der Mittelpunkt der Punkt, der auf halbem Weg zwischen den beiden Punkten. Diese Idee der halben Strecke steht im Einklang mit den geometrischen Proportionalitätssätzen.

Der Mittelpunkt ist ein geordnetes Paar, das auf halbem Weg zwischen zwei gegebenen Punkten liegt. Das ist das Erste, was Sie wissen müssen: Manche Leute halten fälschlicherweise eine Menge für den Mittelpunkt, aber in Wirklichkeit handelt es sich um ein geordnetes Paar.

Der Mittelpunkt für die gegebenen Punkte \((x_1, y_1)\) und \((x_2, y_2)\) wird durch die folgende Formel bestimmt:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]

Erläuterung der mittelpunktsformel

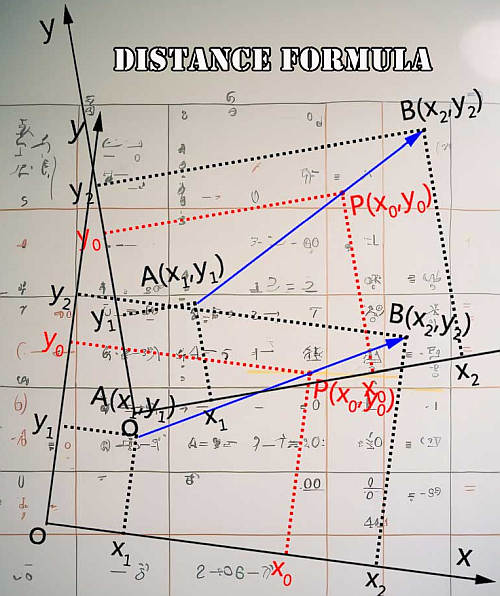
Definition Der Formel: Die obige Mittelpunktsformel steht in engem Zusammenhang mit der entfernungsformel . Die obige Formel besteht ganz einfach darin, dass sie den Durchschnitt der beiden entsprechenden Koordinaten bildet.

Das heißt, die erste Koordinate des Mittelpunkts ist der Durchschnitt der ersten Koordinaten der beiden gegebenen Punkte, und die zweite Koordinate des Mittelpunkts ist der Durchschnitt der zweiten Koordinaten der beiden gegebenen Punkte. Wie kann man die obige Formel anwenden? Bitte sehen Sie sich die folgenden Beispiele an.

Wofür verwende ich die mittelpunktsformel?

Der Begriff "Mittelpunkt" ist uns so vertraut, weil er eng mit der Idee des "halben Weges" von einem Punkt zum anderen verbunden ist. Solche Situationen sind im wirklichen Leben sehr häufig, wenn wir zum Beispiel etwas teilen wollen.

Natürlich muss der Prozess des Teilens von etwas nicht zwangsläufig einen Mittelpunkt beinhalten, aber bei einer gleichwertigen Teilung ist das normalerweise der Fall.

Die Mittelpunktsformel ist also auch deshalb so nützlich, weil sie eine Möglichkeit ist, um mit Hilfe der Abstandsformel in einem sehr speziellen Fall, in dem der gesuchte Punkt gleich weit von den beiden angegebenen Punkten entfernt ist.

Beispiele für mittelwertformeln

Angenommen, wir haben zwei Punkte \((1, 3)\) und \((4, 8)\), dann wird die Mittelpunktsformel wie folgt berechnet:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{1 + 4}{2}, \frac{3+ 8}{2} \right) = \left( \frac{5}{2}, \frac{11}{2} \right) \]

Manchmal lässt man die Antwort als Bruch stehen, oder man wird angewiesen, die Antwort mit Dezimalzahlen zu berechnen. In diesem Fall wäre der Mittelpunkt im vorherigen Beispiel (2,5, 5,5).

Weitere midpoint-beispiele

Wie geht man mit der Mittelpunktsformel bei Brüchen um? Es ist das gleiche Verfahren. Angenommen, wir haben zwei Punkte \((\frac{1}{2}, \frac{1}{4})\) und \((\frac{3}{5}, \frac{3}{4})\), dann wird der Mittelpunkt wie folgt berechnet:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = \left( \frac{1/2 + 3/5}{2}, \frac{1/4+ 3/4}{2} \right) = \left( \frac{11/10}{2}, \frac{1}{2} \right) = \left( \frac{11}{20}, \frac{1}{2} \right) \]

Hat das etwas mit pythagoras zu tun?

Fast alles hat zu tun mit Pythagoras . Bei einem rechtwinkligen Dreieck wird der Mittelpunkt der Hypotenuse auf den Mittelpunkt der Schenkel projiziert. Sie können auch die beiden Punkte nehmen und die abstand zwischen ihnen unter Verwendung der Pythagoras-Formel.