Como usar esta Calculadora de Teorema de Pitágoras

1. Tem três caixas onde pode introduzir dados
2. As formas representam os lados a e b, e a hipotenusa c
3. Por favor escreva os valores de DOIS dessas caixas
4. Por exemplo, se sabe que os lados são a = 3 e b = 4, então digite 3 na primeira forma, e 4 na segunda caixa
5. Ou, por exemplo, se sabe que a hipotenusa é c = 10/3 e o lado a é 5, então digite 5 na primeira forma, e 10/3 na terceira caixa e deixe a segunda caixa vazia

fórmula do teorema de pitágoras

A fórmula básica de Pitágoras é

\[\large a^2 + b^2 = c^2\]

e esta fórmula diz-lhe como encontrar "c" se souber "a" e "b".

Mas também pode encontrar "a" se souber "c" e "b", e pode resolver "b" se souber "c" e "a".

Como se resolve triângulos rectos

Esta Calculadora do Teorema de Pitágoras mostrar-lhe-á todas as etapas do cálculo da fórmula do teorema de Pitágoras.

Esta não é apenas uma calculadora de hipotenusa, pois também pode fornecer um lado e a hipotenusa, e a calculadora mostrar-lhe-á todos os passos para obter o outro lado.

A aplicação mais típica é aquela em que se tem dois lados num triângulo direito, e se pretende obter a hipotenusa. Mas, em última análise, a ideia num triângulo direito é que se tiver dois lados (em geral), pode obter o terceiro lado usando uma versão da fórmula de Pitágoras.

Assim, com duas peças de informação, pode encontrar o comprimento do lado em falta.

Será isto apenas uma calculadora triangular direita

Sim, é. Esta calculadora trata apenas de triângulos rectos. Se o seu triângulo não estiver correcto, pode usar esta Calculadora SAS Triangular (onde se fornecem dois lados e um ângulo, que pode ser qualquer ângulo, não necessariamente 90 ^o .), isto Calculadora do triângulo SSS (onde se conhecem os três lados e se quer encontrar todos os ângulos).

Ou, poderia isto Calculadora AAS Triangular (onde se conhecem dois ângulos e o lado oposto).

Como é que se calcula o teorema de Pitágoras?

Passo 1: Em primeiro lugar, é necessário avaliar a informação de que se dispõe. Tem os dois lados a e b, e está à procura da hipótese c? Ou conhece as hipóteses c e a, ou c e b?

Passo 2: Se conhece os dois lados a e b, esta calculadora de hipotenusa obterá a hipotenusa usando a seguinte fórmula

\[c = \sqrt{a^2 + b^2}\]

e é assim que se encontra a hipotenusa.

Passo 3: Se conhece um lado e a hipotenusa, digamos que conhece a e c, agora a calculadora vai ficar com o outro lado, b, usando a seguinte fórmula

\[b = \sqrt{c^2 - b^2}\]

O ângulo da calculadora do teorema de Pitágoras

Esta calculadora exige que um dos ângulos seja de 90 ^o para que a fórmula pitagórica seja válida.

Pode usar Pitágoras para ângulos? Não, repare que esta calculadora pitágorica apenas trata de lados, e não calcula ângulos.

Se quiser resolver completamente um triângulo (resolver um triângulo significa encontrar lados e ângulos), pode utilizá-los: Calculadora SAS Triangular , Calculadora do triângulo SSS e Calculadora AAS Triangular .

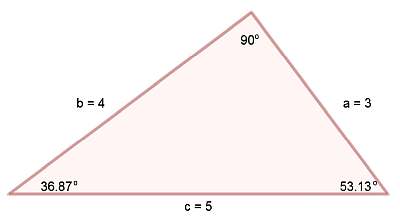
Exemplo de cálculo de um triângulo rectângulo

Pergunta: Assumir que os lados de um triângulo rectângulo são a = 3 e b = 3. Utilizar o Teorema de Pitágoras para calcular a hipótese c.

Solução: Foram-nos fornecidos dois lados, <\(a =\displaystyle3\) e \(b = \displaystyle 6\)>>. Precisamos de utilizar a fórmula pitagórica para calcular a hipótese de utilização <\(c\)>>>.

Com base nesta informação, a seguinte fórmula pitagórica precisa de ser utilizada:

\[c = \displaystyle\sqrt{a^2 + b^2}\]

Assim sendo, agora, ligando os valores que temos disponíveis, obtém-se o seguinte:

\[c = \displaystyle\sqrt{a^2 + b^2} = \displaystyle\sqrt{3^2 + 6^2} = \displaystyle\sqrt{9 + 36} = \displaystyle\sqrt{45} = 3\sqrt{5}\]

Portanto, e resumindo, descobrimos que <\(a = 3\), \(b = 6\) e \(c = 3\sqrt{5}\)>>.