Álgebra Tutoriais

O Teorema Binomial

O Teorema Binomial é um dos teoremas mais famosos da Álgebra e tem uma infinidade de aplicações nas áreas de Álgebra, Probabilidade e Estatística. Ele afirma uma fórmula agradável e concisa para o n ^º potência da soma de dois valores: $(a+b)^n$

Fui apresentado pela primeira vez informalmente por Sir Isaac Newton em 1665.

Muitos outros matemáticos notáveis abordaram o teorema Binomial após Newton. Foi um problema muito atraente nos séculos XVII e XVIII.

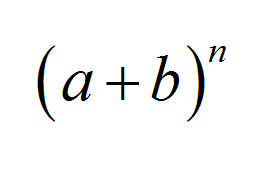
A Fórmula para a Expansão Binomial

O que é inteiro sobre o Teorema Binomial é que ele fornece uma fórmula muito elegante e concisa. Antes de entrar na fórmula, façamos alguns cálculos. Por exemplo, para $n = 2$ , obtemos:

\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2

\large = a^2 + 2ab + b^2

Agora vamos tentar com $n = 3$ :

\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b)

\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3

\large = a^3 + 3a^2b + 3ab^2 + b^3

Finalmente, sejamos corajosos e experimentemos com $n = 4$ :

\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b)

\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4

\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4

Ok, isso foi corajoso, não é? Você vê algum padrão lá. Eu posso ver alguns. Por exemplo, para $n = 2$ , podemos simplificar para 3 termos. Para $n = 3$ podemos simplificar para 4 termos, e para $n = 4$ podemos simplificar para 5 termos. Portanto, em geral, espero que para o poder geral de $n$ , teremos $n+1$ termos

Mais padrões? Bem, sempre há um termo da forma $a^l b^m$ , e podemos ver que os poderes $l$ vão diminuindo, e os poderes $m$ vão aumentando. Mas há algo interessante também: Se você verificar cada termo, a soma dos poderes é sempre $n$ . Na verdade, você verificará $l + m = n$ para todos esses termos.

Por exemplo, para $n = 2$ você tem o termo $2 a b$ . A potência de $a$ é 1 e a potência de $b$ é 1, e a soma das potências é $1 + 1 = 2$ . Ou, por exemplo, para $n = 4$ você tem o termo $6 a^2 b^2$ , onde a potência de $a$ é 2 e a potência de $b$ é 2, e a soma das potências é $2 + 2 = 4$

O Teorema Binomial Geral

Agora estamos prontos para fornecer a expressão geral para o Teorema Binomial. Pronto? Nós temos:

\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n

onde o termo ${n \choose i}$ é lido como "n escolher i" ou também como um "coeficiente combinatório", e é definido como

\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}

Por exemplo,

\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10

Você pode usar isso calculadora de coeficiente combinatório para aprender mais sobre ele e praticar vendo todas as etapas mostradas.

O Teorema Binomial Geral usando uma Soma

A soma acima que define o Teorema Binomial usa a notação por extensão, para tornar os termos mais compreensíveis. Como sempre em matemática, tentamos tornar as coisas mais compactas e a expressão acima pode ser resumida como:

\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i}

Observe os poderes dos termos na expansão. O termo geral é $a^i b^{n-i}$ (vezes uma constante). A soma dos poderes é $i + (n-i) = n$ . Portanto, a soma das potências de TODOS os termos na expansão deve ser $n$ . Não é bonito ???

EXEMPLO 1

O termo $x^3 y^2$ (vezes uma constante) pode fazer parte da expansão de $(x+y)^6$ ? Por quê?

RESPONDA:

A resposta é não. Neste caso, $n = 6$ , e sabemos pelo teorema Binomial que a soma das potências dos termos $x^l y^m$ na expansão deve ser igual a $n$ . Nesse caso, $l + m = 3 + 2 = 5$ , que não é o mesmo que $n = 6$ . Portanto, o termo $x^3 y^2$ (vezes uma constante) não pode fazer parte da expansão de $(x+y)^6$ .

EXEMPLO 2

Expanda $(a-b)^3$ usando o teorema Binomial.

RESPONDA:

Esperar. Você deve estar pensando "Você acabou de me ensinar como expandir $(a+b)^n$ , mas agora você me pergunta sobre $(a-b)^n$ . Por que você é tão cruel". Aguente. Eu não estou pregando peças em você.

Sempre tem um truque (não se esqueça dessa linha, ela aparece muito no Math).

Observe que $a - b$ é igual a $a + (-b)$ .

Ahhhhhhh, então o Teorema Binomial ainda se aplica. Então:

\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3

\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3

\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3

\large = a^3 - 3 a^2 b + 3 a b^2 -b^3

Mais sobre a expansão binomial

O teorema Binomial é tão importante que é abordado em quase todos os cursos, incluindo Álgebra, Cálculo, Probabilidade e Estatística.

Existem algumas generalizações, como a expansão binomial negativa, que está além do escopo deste tutorial.

O Triângulo Pascal

Algumas vezes os alunos ficam presos quando precisam calcular as constantes (os coeficientes combinatórios) que fazem parte da expansão binomial. Uma maneira realmente fácil de fazer isso é usar o Triângulo de Pascal.

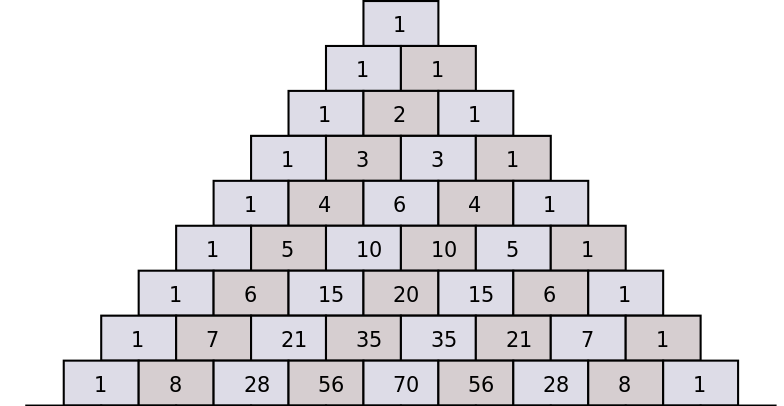
O triângulo Pascal mostra como os coeficientes binomiais sucessivos podem ser calculados com base nos coeficientes do valor anterior de $n$ , adicionando os dois coeficientes que vêm imediatamente acima.

Formulários

A expansão binomial tem múltiplas aplicações na Álgebra e na Teoria das Probabilidades. Por exemplo, em Probabilidade, a distribuição Binomial é baseada no teorema binomial.

Na verdade, considere um número $0 \le p \le 1$ . Então, $p + (1-p) = 1$ e podemos usar o teorema Binomial:

\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i}

o que significa que

\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1

Acontece que cada um dos termos ${n \choose i} p^i (1-p)^{n-i}$ representa uma probabilidade. Além disso, temos:

\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1

onde $X$ é o número de sucessos após $n$ tentativas, quando a probabilidade de sucesso de cada tentativa é $p$ . A variável $X$ é conhecida como variável aleatória binomial.