Calculadora de frações
Instruções: Use esta calculadora de fração para calcular qualquer operação ou cálculo de fração que você fornecer, mostrando todas as etapas. Por favor, digite o cálculo da fração que deseja realizar na caixa de formulário abaixo.
Mais sobre esta calculadora de frações
Esta calculadora permitirá que você adicionando frações , multiplicando frações , frações de divisão , etc., e qualquer operação de fração válida, mostrando todas as etapas. Você precisa fornecer uma expressão válida envolvendo frações. Pode ser algo simples como '1/2 + 1/3', ou algo mais complexo como '(1/3+1/4)(1/5+1/6)'.
Depois de fornecer uma expressão válida envolvendo fração, basta clicar no botão "Calcular" e você receberá todas as etapas dos cálculos.
A álgebra de frações envolve a conversão de frações, como o uso de denominador comum e o uso de regras aritméticas básicas. Em suma, o processo de cálculo pode ser trabalhoso, embora possa ser feito sistematicamente, sem grandes problemas.
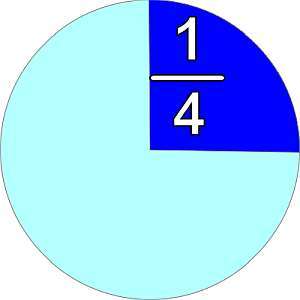
Como calculo frações
Para calcular frações você utilizará uma metodologia muito simples e direta, que dependerá da operação (adição, subtração, multiplicação ou divisão) que deseja realizar. Cada operação terá sua própria lógica.
Em termos simples, adições e subtrações exigem encontrar um denominador comum , enquanto a multiplicação e a divisão operam diretamente numeradores e denominadores. Mais detalhes sobre isso nos parágrafos abaixo.
Como somar frações?
A adição de frações é uma das habilidades mais cruciais e básicas que você usará ao calcular operações fracionárias. Normalmente, você precisa começar encontrando um denominador comum, mas muitas vezes você usará a seguinte fórmula para adição de frações:
\[\displaystyle \frac{a}{b} + \frac{c}{d} = \displaystyle \frac{ad + cb}{bd} \]Quais são os passos para adicionar frações?
- Passo 1: Identifique o numerador e o denominador para a primeira e segunda fração
- Passo 2: Suponha que a e b são o numerador e denominador da primeira fração, e c e d são o numerador e denominador da segunda fração
- Passo 3: Use a fórmula de adição: A fração resultante tem ad + cb como numerador e bd como denominador
A subtração de frações é derivada apenas pela soma de frações: Para subtrair duas frações, basta multiplicar a segunda por -1 e adicioná-la à primeira .
Como multiplicar frações?
A segunda pedra angular para realizar cálculos gerais de frações é a multiplicação de frações. Nesse caso, não há necessidade de encontrar um denominador comum, você apenas multiplicará os numeradores e denominadores entre si:
\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]Quais são os passos para multiplicar frações?
- Passo 1: Identifique o numerador e o denominador para a primeira e segunda fração
- Passo 2: Suponha que a e b são o numerador e denominador da primeira fração, e c e d são o numerador e denominador da segunda fração
- Passo 3: Use a fórmula de adição: A fração resultante tem ad + cb como numerador e bd como denominador
Semelhante ao que aconteceu com adição e subtração, a divisão de frações é derivada apenas da multiplicação de frações: Para dividir duas frações, basta multiplicar a primeira pela fração inversa da segunda (a fração inversa é obtida trocando o numerador pelo denominador na fração).
Decimais para frações
Você pode converter qualquer decimal em fração usando um truque simples. Alguns decimais serão mais fáceis de converter, especificamente aqueles que possuem um número finito de decimais. Decimais periódicos também podem ser convertidos. Estas são as etapas a seguir:
- Passo 1: Identifique o tipo de número com o qual você está trabalhando e identifique se ele possui dígitos decimais ou não. Se D tiver decimais, avalie quantos decimais ele possui
- Passo 2: Se D não tiver decimais, a conversão para fração é direta, como sabemos \(D = \frac{D}{1}\)
- Etapa 3: se D tiver um número finito de dígitos decimais, digamos que ele tenha k decimais. Caso você multiplique D por \(10^k\) para eliminar os decimais, encontre esse \(D = \frac{D \times 10^k}{10^k}\) e reduza a fração conforme necessário.
- Passo 4: Se D tem um número infinito de decimais, então é periódico, você faz o seguinte truque: Multiplique o número por uma potência de 10 que ao fazer 10D - D elimina a periodicidade, e então você obtém que 9D é finito decimal, com o qual você lida na Etapa 3.
Por exemplo, você poderia perguntar o que é 1,214285714 como fração e notamos que D = 1,214285714 tem 9 dígitos decimais. Então observamos que
\[D = 1.214285714 = \frac{1.214285714 \times 10^9}{10^9} = \frac{1,214,285,714}{1,000,000,000} = \frac{607,142,857}{500,000,000} \]Para um número de período, digamos que você tenha D = 2,349999999.... A parte periódica começa na terceira posição decimal, então multiplicamos D por 100. Obtemos 100D = 234,999999....
Agora, subtraímos D de 100D e obtemos \(100D - D = 234.999999.... - 2.349999 = 232.65\), o que implica que \(99D = 2.3265\), que pode ser processado da seguinte forma:
\[99D = 232.65 \Rightarrow 9900D = 23265 \Rightarrow D = \frac{23265}{9900} = \frac{47}{20} \]Relação entre porcentagens e frações
Como você provavelmente suspeita, porcentagens e frações estão intimamente relacionadas. Por exemplo, uma porcentagem de 80% é simplesmente 0,80, que é um decimal, e usando as etapas acima você pode convertê-la diretamente em fração.
Então, como os decimais e as frações estão intimamente relacionados, Calculadora De Porcentagem e um Calculadora de Frações também estão intimamente relacionados.
Por que se preocuparia em calcular frações?
As frações são uma das pedras angulares da álgebra e de qualquer expressão algébrica para calcular . Frações são operandos simples, mas que podem ser compostos em termos mais complicados usando operações como soma, multiplicação, etc., e então usando funções podemos construir expressões ainda mais avançadas.
O centro de todas as calculadoras algébricas começa com o poder dos números básicos das frações.
Exemplo: calculando a soma das frações
Calcule o seguinte: \(\frac{1}{3} + \frac{5}{4} - \frac{5}{6}\)
Solução:
Precisamos calcular e simplificar a seguinte expressão: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\).
Obtém-se o seguinte cálculo:
que conclui o cálculo.
Exemplo: outro cálculo de fração
Calcule \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).
Solução:
Precisamos calcular e simplificar a seguinte expressão: \(\displaystyle \left(\frac{2}{3}\cdot\frac{6}{5}\right)+\frac{2}{5}\).
Obtém-se o seguinte cálculo:
que conclui o cálculo.
Outras calculadoras de fração úteis
Cálculos fracionários são cruciais em Álgebra. Outras operações úteis incluem simplificando uma fração reduzindo a seus termos mais baixos. Também, você pode converter fração em porcentagem ou fracção até à decimal , pois esses têm uma conexão íntima.
Além disso, você pode estar interessado em um calculadora de fração mista , dependendo da sua configuração de aprendizado. Em configurações mais elementares, os números mistos são tratados como entidades importantes, enquanto em configurações mais avançadas, os números mistos são apresentados apenas em sua notação fracionária.




