Come funziona una calcolatrice di regressione logaritmica

Questa calcolatrice ti consentirà di stimare una regressione logaritmica per i dati campione forniti nel foglio di calcolo di input dati corrispondente.

Se vengono forniti dati validi (in questo caso, la variabile X può assumere solo valori positivi), dopo aver cliccato su "Calcola", verrà visualizzata un'esecuzione dei passaggi coinvolti nel processo, nonché un grafico a dispersione che mostrerà la qualità dell'adattamento.

Si noti che quando i dati sono dimensionalmente validi, è sempre possibile eseguire una regressione logaritmica, ma ciò non significa che i risultati saranno di buona qualità, almeno in termini di adattamento.

Strumenti e calcolatrici per la regressione logaritmica

Esistono diversi strumenti che puoi usare per stimare la tua regressione logaritmica. In teoria, puoi procedere manualmente, usando una trasformazione logaritmica usando una normale calcolatrice (anche quelle che hai con il telefono), e poi usare un'equazione ausiliaria dei minimi quadrati per trovare il modello logaritmico, che è

\[ Y = a + b \ln(X) + \varepsilon \]

Di sicuro, l'approccio "farlo a mano" potrebbe essere noioso e soggetto a errori, per usare un eufemismo. Ecco perché è un'ottima opzione usare questo Calcolatrice di regressione logaritmica , perché fa tutto il lavoro per te e ti mostra tutti i passaggi

Esistono altri strumenti, come le app per telefoni cellulari, che dovrebbero eseguire tutti i tipi di regressione, ma dovrai provare e vedere perché la situazione potrebbe essere incerta.

Passaggi per eseguire una regressione logaritmica

• Passo 1: Elencare chiaramente la variabile indipendente (X) e la variabile dipendente (Y) e assicurarsi che entrambe le variabili abbiano la stessa dimensione del campione
• Passo 2: Assicurati che i tuoi valori di X siano positivi, altrimenti non puoi eseguire la regressione
• Passaggio 3: Costruisci una nuova variabile indipendente X* = ln(X) applicando la trasformazione del logaritmo naturale
• Passaggio 4: Ora esegui un'analisi di regressione lineare regolare per X* rispetto a Y

Una cosa da tenere a mente è che è assolutamente consigliabile utilizzare una calcolatrice o un software per ottenere statistiche diagnostiche che ti aiuteranno a valutare se ha senso o meno utilizzare il modello di regressione logaritmica .

Utilizzo di excel rispetto ai calcolatori dedicati alla regressione logaritmica

Excel svolge un ruolo importante nell'aiutarti a condurre analisi statistiche di base: fornisce un'interfaccia pulita e collaudata per eseguire test di base, incluso il calcolo della regressione logaritmica.

Il problema principale di Excel è che non fornisce il passaggio delle soluzioni. Questo potrebbe aiutare con l'avvento di framework AI come Copilot, che probabilmente doterebbero Excel di passaggi descrittivi del calcolo.

Comprensione e interpretazione dei risultati del calcolatore di regressione

Come ogni altro Analisi di regressione , per il caso logaritmico non è diverso in quanto darai un'occhiata alle statistiche di adattamento del modello, come Statistiche F per testare la significatività del modello nel suo complesso, e t-statistiche per la significatività individuale dei predittori .

Inoltre, probabilmente vorrai dare un'occhiata alla variazione e all'errore spiegati e al Coefficienti R^2 e R^2 aggiustati , che fornirà stime della variazione spiegata della variabile dipendente dal modello.

Esempi di regressione logaritmica

Considerare le variabili

X: 1, 2, 3, 4, 5

E: 15, 25, 28, 29, 30

Stimare un modello di regressione logaritmica.

Soluzione:

I seguenti dati per le variabili X e Y vengono forniti per costruire un modello di regressione logaritmica:

X	Y
1	15
2	25
3	28
4	29
5	30

La variabile indipendente che utilizzeremo è il logaritmo naturale di X, e la variabile dipendente è Y. Per calcolare i coefficienti di regressione per questa regressione ausiliaria, è necessario utilizzare la seguente tabella:

	X	Z = ln(X)	Y	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

Sulla base della tabella soprastante, si calcola quanto segue:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

Pertanto, sulla base dei calcoli di cui sopra, i coefficienti di regressione (la pendenza \(m\) e l'intercetta y \(n\)) si ottengono come segue:

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

Pertanto, troviamo che l'equazione di regressione è:

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

Ma poiché la variabile ausiliaria è \(Z = \ln(X)\), concludiamo che l'equazione di regressione logaritmica è:

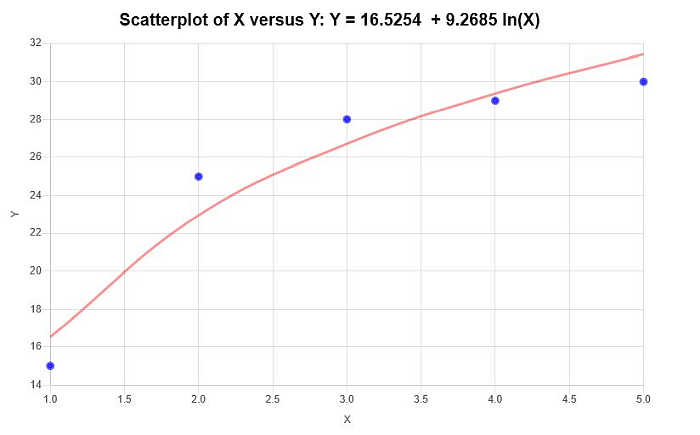
\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

Pertanto, sulla base delle informazioni fornite sopra, si ottengono i seguenti diagrammi di dispersione e di regressione:

Altri calcolatori di statistica

Potrebbe interessarti anche calcolo di una regressione esponenziale , o elaborando le sottigliezze di un Regressione polinomiale , ognuno dei quali si applica in contesti diversi, in base al comportamento dei dati campione osservati.

Probabilmente vorrai costruire un grafico a dispersione per valutare il comportamento empirico dei dati e per valutare in anticipo se è applicabile una regressione logaritmica invece di un diverso tipo di regressione.