Calcolo dell'elasticità della domanda rispetto al prezzo a partire da dati campione

Utilizza questa calcolatrice per stimare l'elasticità della domanda rispetto al prezzo in base ai dati campione relativi a prezzo e quantità domandata da te forniti.

Dovrai fornire dati campione validi, in termini di entrambi i campioni (prezzo e quantità richiesta) come valori positivi. Una volta incollati i dati nel foglio di calcolo, puoi cliccare su "Calcola" per ottenere tutti i passaggi mostrati.

Si noti che questo approccio richiede che i dati seguano uno schema specifico adatto a un modello logaritmo-logaritmo, in cui \(\ln(P)\) e \(\ln(Q)\) vengono utilizzate come variabili ausiliarie per condurre un modello di regressione lineare.

Calcolo dell'elasticità del prezzo da dati campione

Per calcolare l'elasticità del prezzo, sarà necessario stimare il seguente modello ausiliario:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Si noti che ciò corrisponde a un modello di regressione lineare regolare con le variabili originali prezzo e quantità trasformate in logaritmo. Ecco perché richiediamo che entrambe le variabili siano strettamente positive.

Quali sono i passaggi per calcolare l'elasticità?

• Passo 1: Identificare i dati campione per le variabili fornite per prezzo (P) e quantità (Q)
• Passo 2: Assicurati che entrambi i campioni abbiano la dimensione del campione e che siano ENTRAMBI positivi, altrimenti non sarai in grado di eseguire il calcolo
• Passaggio 3: Trasforma logaritmicamente entrambe le variabili: calcola ln(X) e ln(Y)
• Passaggio 4: Eseguire una regressione lineare ausiliaria per le variabili ln(X) e ln(Y), dove ln(X) è la variabile indipendente e ln(Y) è la variabile dipendente
• Passaggio 5: Il coefficiente di pendenza trovato per questa regressione ausiliaria è l'elasticità della domanda rispetto al prezzo per questi dati

Il passaggio cruciale è quindi la trasformazione logaritmica dei dati, che consente di calcolare l'elasticità sulla base dei risultati di una regressione lineare, rendendo i risultati ottenuti altamente interpretabili.

Comprendere l'elasticità del prezzo

Per definizione, l'elasticità del prezzo è definita utilizzando la seguente formula:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Ciò indica che, tra le altre cose, possiamo prevedere la variazione percentuale della domanda di quantità utilizzando la seguente espressione:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Ciò indica che la variazione percentuale di Q è la stessa della variazione percentuale di P moltiplicata per l'elasticità. È importante notare che questa definizione si applica puntualmente : ovvero, l'elasticità non deve essere costante lungo tutta la curva di domanda. Sebbene possa esserlo, e in questa calcolatrice si fa tale ipotesi.

Interpretazione dei coefficienti di elasticità del prezzo

Come abbiamo visto nella sezione precedente, l'elasticità \(\varepsilon\) corrisponde semplicemente al coefficiente di pendenza della regressione logaritmica ausiliaria trasformata. Ma ha anche un'interpretazione molto interessante della variazione marginale:

• Per una variazione aggiuntiva dell'1% del prezzo, la domanda di quantità cambia di \(\varepsilon \%\)

Questo è esattamente ciò che è richiesto e implicito dalla formula di elasticità. Osserva che questa calcolatrice stima un modello che presuppone che i dati seguano uno schema che conduce a un'elasticità costante, il che non è il caso di una funzione di domanda lineare, ad esempio.

Fattori che influenzano l'elasticità del prezzo

L'elasticità è un riflesso della reazione dei consumatori alle variazioni di prezzo. In genere, l'elasticità è negativa: se il prezzo di un bene aumenta, l'acquirente probabilmente ne comprerà di meno, almeno se abbiamo un bene normale.

Un'elasticità maggiore di 1 in valore assoluto (inferiore a -1) si dice associata a una reazione elastica al prezzo, mentre un'elasticità compresa tra 0 e 1 in valore assoluto (tra -1 e 0) si dice associata a una reazione anelastica al prezzo.

La teoria economica prevede che diversi fattori influenzeranno l'elasticità della domanda rispetto al prezzo. Ad esempio, l'assenza o la carenza di sostituti porterà a una maggiore elasticità in valori assoluti.

Calcolo dell'elasticità del campione: utilizzo dei dati campione

Calcolare l'elasticità dai seguenti dati campione:

P	Q
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

Soluzione : Per trovare l'elasticità della domanda rispetto al prezzo da questi dati, dobbiamo costruire un modello di regressione logaritmica, in cui la variabile indipendente che utilizzeremo è \(ln(P)\) e la variabile dipendente è il logaritmo naturale di \(ln(Q)\)

Per calcolare i coefficienti di regressione per questa regressione ausiliaria, è necessario utilizzare la seguente tabella:

	P	Z = ln(P)	Q	La = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

Sulla base della tabella soprastante, si calcola quanto segue:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Pertanto, sulla base dei calcoli di cui sopra, i coefficienti di regressione (la pendenza \(m\) e l'intercetta y \(n\)) si ottengono come segue:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Pertanto, troviamo che l'equazione di regressione è:

\[W = 2.1639 + 0.715 \text{ Z}\]

Ma poiché le variabili ausiliarie sono \(Z = \ln(X)\) e \(W = \ln(Y)\), concludiamo che l'equazione di regressione logaritmica è:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Pertanto, sulla base delle informazioni fornite sopra, si ottengono i seguenti diagrammi di dispersione e di regressione:

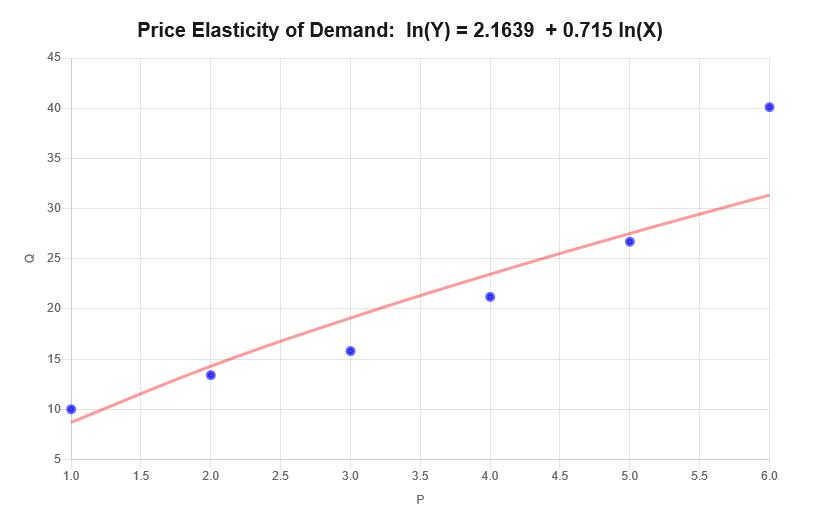
Interpretazione

L'elasticità in questo caso corrisponde al coefficiente di pendenza per i dati forniti, ovvero \(\varepsilon = 0.715 \), che può essere interpretato come segue:

• Per un aumento dell'1% del prezzo, si verifica un aumento medio dello 0,715% della quantità domandata.

Calcolatrici più interessanti

La stima dei modelli da dati campione è un'abilità cruciale necessaria sia in statistica che in economia. Utilizzare dati campione per calcolare un modello di regressione è una delle applicazioni più comuni dell'utilizzo di dati campione per la creazione di modelli.

Ma spesso accade che un modello lineare regolare non si adatti sufficientemente bene ai dati, per cui dobbiamo tentare diverse strutture funzionali. Ad esempio, potremmo potenzialmente stimare un Regressione logaritmica , UN regressione logaritmica o un Regressione polinomiale , solo per citarne alcuni, che potrebbero essere più efficaci nello spiegare la variazione della variabile dipendente rispetto alla regressione regolare.

L'opzione di calcolo dell'elasticità da dati campione è utilizzato principalmente in un contesto esplorativo. Più spesso che no, il l'elasticità è calcolata direttamente dalla funzione di domanda , quando disponibile. In altre circostanze, l'elasticità è stimata da una coppia di punti di domanda-prezzo utilizzando il formula di elasticità dell'arco .