Domanda 1: Le formule per la linea dei minimi quadrati sono state trovate risolvendo il sistema di equazioni

\[nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

Risolvi queste equazioni per b e m per dimostrarlo

\[\begin{align} & m=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left(\sum{{{x}^{2}}} \right)-{{\left( \sum{x} \right)}^{2}}} \\ & b=\frac{\sum{y-m\left( \sum{x}\right)}}{n} \\ \end{align}\]

Soluzione: A partire dal

\[ nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

abbiamo due equazioni e due incognite (me b)

Lo otteniamo moltiplicando la prima equazione per \(\left( \sum{x} \right)\) e la seconda per -n otteniamo

\[\begin{align} & nb\left( \sum{x} \right)+m{{\left( \sum{x} \right)}^{2}}=\left( \sum{y}\right)\left(\sum{x} \right) \\ & -nb\left( \sum{x} \right)-mn\left( {{\sum{x}}^{2}}\right)=n\sum{xy} \\ \end{align}\]

e ora aggiungendo questi:

\[m\left( {{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right) \right)=\left( \sum{x} \right)\left(\sum{y} \right)-n\left( \sum{xy} \right)\]

\[\Rightarrow \,\,\,\,m=\frac{\left( \sum{x} \right)\left( \sum{y} \right)-n\left( \sum{xy} \right)}{{{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right)}=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left( {{\sum{x}}^{2}} \right)-{{\left( \sum{x} \right)}^{2}}}\]

Ora, da questa equazione:

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\]

possiamo risolvere per b :

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\,\,\Rightarrow \,\,\,nb=\left( \sum{y} \right)-m\left( \sum{x} \right)\,\Rightarrow \,\,\,b=\frac{\left( \sum{y} \right)-m\left( \sum{x} \right)}{n}\]

Domanda 2: Determinare il coefficiente di correlazione e fare un grafico della linea di regressione con il coefficiente di regressione per il seguente insieme di dati.

Incendi boschivi e acri bruciati. Il numero di incendi e il numero di acri bruciati sono i seguenti

Incendi (x)	72	69	58	47	84	62	57	45
Acri (y)	62	41	19	26	51	15	30	15

Soluzione: (a) Si ottiene il seguente grafico a dispersione:

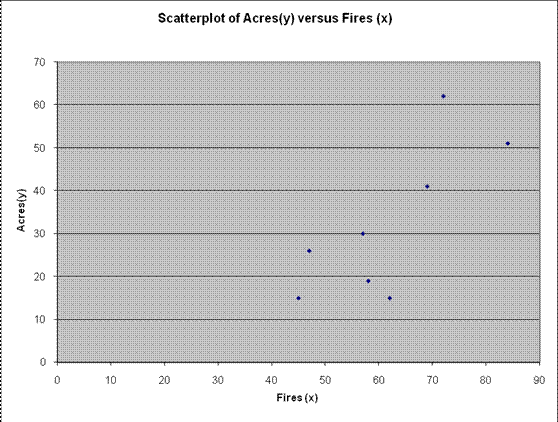
Sulla base del grafico a dispersione sopra, osserviamo che esiste un grado da moderato a forte di associazione lineare positiva.

(b) D'altra parte, abbiamo la seguente tabella che mostra i calcoli necessari per calcolare la correlazione di Pearson: Otteniamo

La correlazione di Pearson r è calcolata come

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {17216}-{494}\times {259}}{\sqrt{8\times {31692}-{494}^{2}}\sqrt{8\times 10513-{259}^{2}}}\]

\[=0.7692\]

(c) Il coefficiente di determinazione è

\[{{r}^{2}}={0.7692}^{2}= {0.5917}\]

il che significa che il 59,17% della variazione in Acres (y) è spiegato da Fires (x).

(d) Vengono calcolati i coefficienti di regressione

\[b=\frac{n\left( \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \right)-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}=\frac{8 \times {17216}-{494}\times {259}}{8 \times {31692}-{494}^{2}}= 1.0297\]

and

\[a=\bar{y}-b \bar{x}={32.375}{+} {1.0297}\,\cdot \, {61.75} = {-31.208}\]

Ciò significa che l'equazione di regressione è

\[\hat{y}= {-31.208}{+}{1.0297}\,x\]

Graphically:

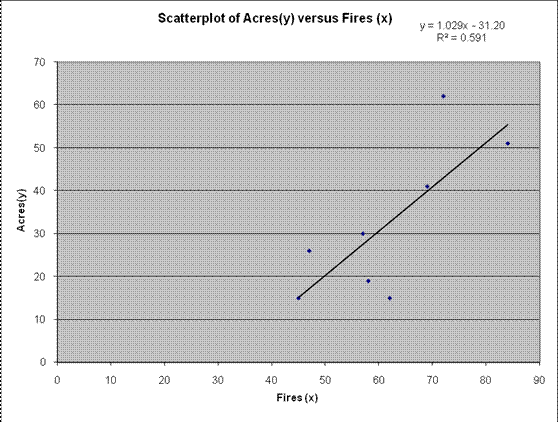
Domanda 3: Hai condotto uno studio per determinare se il tempo medio trascorso nel laboratorio informatico ogni settimana e il voto del corso in un corso di computer fossero correlati. Utilizzando i dati forniti di seguito, quale conclusione trarresti su questo problema?

student	# hours in lab	Course Grade
1	20	96
2	11	51
3	16	62
4	13	58
5	89
6	15	81
7	10	46
8	10	51

Soluzione: La tabella seguente mostra i calcoli necessari per calcolare Pearson correlazione r : Noi abbiamo

La correlazione di Pearson è calcolata come

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {7925}-{112}\times {534}}{\sqrt{8\times {1660}-{112}^{2}}\sqrt{8\times 38224-{534}^{2}}}\]

\[=0.9217\]

Vogliamo verificare la significatività del coefficiente di correlazione. Più specificamente, vogliamo testare

\[\begin{align}{{H}_{0}}:\rho {=} 0 \\ {{H}_{A}}:\rho {\ne} 0 \\ \end{align}\]

Per verificare l'ipotesi nulla, utilizziamo un test t. La statistica è calcolata come

\[t= r \sqrt{\frac{n-2}{1-{{r}^{2}}}}= {0.9217} \times \sqrt{\frac{6}{1-{0.9217}^2}}= {5.8198}\]

Il valore p a due code per questo test viene calcolato come

\[p=\Pr \left( |{{t}_{6}}|>5.8198 \right)=0.0011\]

Dal momento che \(p = 0.0011 {<} 0.05\) , e questo significa che rifiutiamo l'ipotesi nulla H ₀ .

Quindi, abbiamo prove sufficienti per sostenere l'affermazione che la correlazione tra il numero di ore in laboratorio e il grado del corso è buoni diversi da zero.