Maggiori informazioni su questo calcolatore grafico cos

Questa calcolatrice ti consentirà di generare il grafico per qualsiasi funzione coseno, insieme a ampiezza, periodo e frequenza , mostrando tutti i passaggi. Devi fornire una funzione valida che coinvolga la funzione coseno. Potrebbe essere qualcosa di banale come cos(x), oppure puoi renderlo più complicato come 2*cos(1/3 x + pi) - 4/5.

Una volta fornita una funzione valida che coinvolge il coseno, basta cliccare su "Calcola" per ottenere i risultati e tutti i passaggi del processo mostrato.

Il coseno è uno funzione trigonometrica che ha una miriade di applicazioni in matematica e fisica. È molto comunemente usato anche in Geometria, quando risolvere triangoli .

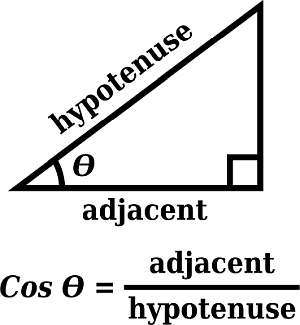
Come fare un cos grafico?

Il principio principale con la rappresentazione grafica di qualsiasi tipo di funzione è ricorrere a una funzione semplice nota per la quale conosciamo il suo grafico, e quindi costruire il grafico che vogliamo trovare in base alle traduzioni e al ridimensionamento di questo semplice grafico.

Per il caso del grafico cos, sappiamo che l'espressione più semplice di una funzione coseno è f(x) = cos(x), che ha un grafico mostrato di seguito:

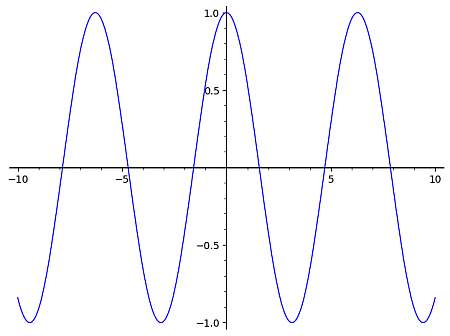
Quindi, possiamo usare questo grafico di base per derivare il grafico di funzioni cos più complesse poiché la forma generale sarà la stessa, solo che può essere potenzialmente traslata a sinistra oa destra, in basso o in alto, e anche il periodo può potenzialmente cambiare, a seconda della funzione fornita.

Quali sono i passaggi per rappresentare graficamente una funzione coseno?

• Passo 1 : Identificare la funzione cos che si desidera rappresentare graficamente nella forma a*cos(bx+c)+d, se possibile
• Passo 2 : Il valore di a corrisponderà a the ampiezza , d sono le unità in cui il grafico del cos di base viene traslato verso l'alto e il grafico viene spostato di -c/b a destra
• Passaggio 3 : Se la funzione cos non è nella forma a*cos(bx+c)+d, creare una tabella di valori per x e f(x) (dove f(x) è la funzione cos data) e calcolare diverse punti che puoi utilizzare per tracciare manualmente la forma del grafico cos

In effetti, solo le funzioni della forma a*cos(bx+c)+d avranno un'espressione chiara per ampiezza, periodo, frequenza e traslazioni, ma non sono le uniche funzioni coseno che puoi concepire. Ad esempio, \(f(x) = cos(x^2)\) è una funzione cos, ma non ha periodo o frequenza, ad esempio.

Grafico cos contro grafico seno?

Quanto sono simili i grafici del coseno e del seno? Beh, abbastanza simile. Per prima cosa, si noti che stiamo parlando del grafico cos di base e del grafico seno, questo è sin(x) e cos(x).

Quindi, il grafico del cos si ottiene semplicemente spostando il grafico del seno a sinistra delle unità \(\pi/2\). Quindi, il grafico cos e il grafico seno sono essenzialmente gli stessi, tranne che per una traslazione.

Grafico cos in gradi

C'è qualche differenza tra il grafico del coseno in radianti e il grafico del cos in gradi? Bene, c'è una differenza di scala, poiché cos completa un intero periodo in \(2\pi\) se misurato in radianti, e completa un intero periodo in 360 ^O se misurato in gradi. Ma in termini di forma, non c'è alcuna differenza essenziale.

Come utilizzare questo calcolatore grafico cos?

Questo calcolatore grafico cos elimina tutte le congetture per te, poiché tutto ciò che devi fare è fornire una funzione cos valida. A seconda del tipo di funzione cos che fornisci, avrai un periodo, o forse il periodo non sarà definito, in un caso come \(f(x) = cos(x^2)\), dove diciamo ancora che abbiamo un funzione cos .

I grafici cos, insieme ai grafici seno e tangente sono tra i più comuni grafici trigonometrici che in genere incontrerai.

Esempio: grafico cos

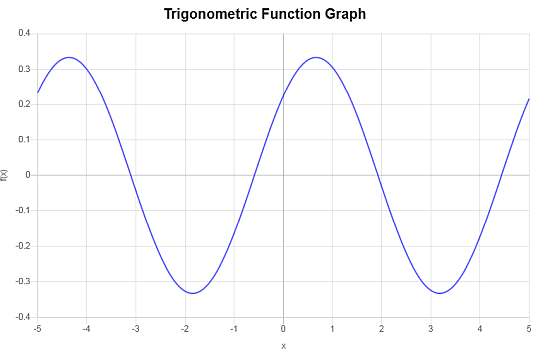
Calcola il grafico di : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Soluzione: È stata fornita la seguente funzione:

\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\]

In base all'argomento della funzione trigonometrica passata, la frequenza e il periodo vengono calcolati come segue:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

e anche

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Pertanto, considerando la funzione trigonometrica fornita, \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\), otteniamo che:

» L'ampiezza in questo caso è \(A = 1/3\).

» Lo sfasamento è uguale a \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

» Lo spostamento verticale è pari a \( 0\).

Riassumendo, per la data funzione trigonometrica è stato trovato quanto segue

• Periodo = \(5.0265\)
• Frequenza = \(0.1989\)
• Ampiezza = \(1/3\)
• Spostamento di fase = \(0.6667\)
• Spostamento verticale = \(\displaystyle 0\)

Quello che segue è il grafico corrispondente

Esempio: più grafici cos

La seguente funzione è periodica? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 - \frac{5}{6}\right)\)

Soluzione: No, non lo è, a causa del termine \(x^2\).

Esempio: grafico del coseno

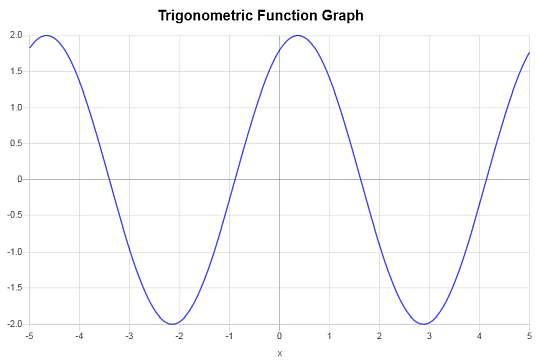
Calcola il grafico di : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Soluzione: Si noti che l'espressione trigonometrica passata può essere semplificata come segue:

quindi la funzione con cui lavoreremo è \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Quindi, in base all'argomento della funzione trigonometrica passata, la frequenza e il periodo vengono calcolati come segue:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

e anche

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Sulla base della funzione trigonometrica fornita, \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\), otteniamo che:

» L'ampiezza in questo caso è \(A = 2\).

» Lo sfasamento è uguale a \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

» Lo spostamento verticale è pari a \( 0\).

Riassumendo, per la data funzione trigonometrica è stato trovato quanto segue

• Periodo = \(5.0265\)
• Frequenza = \(0.1989\)
• Ampiezza = \(2\)
• Spostamento di fase = \(0.3667\)
• Spostamento verticale = \(\displaystyle 0\)

Quello che segue è il grafico corrispondente

Altri calcolatori di geometria

Uno dei più utili che puoi trovare è questo calcolatore di periodo e frequenza , per il quale fornisci qualsiasi funzione trigonometrica e ti verranno forniti l'ampiezza, il periodo e la frequenza.

Inoltre, puoi usare questo calcolatrice del peccato con passaggi lavorare con espressioni trigonometriche più complesse che trattano la funzione seno. Seno e coseno sono davvero la pietra angolare di tutto ciò che è correlato alla geometria e alla trigonometria

Inoltre, forse ti interessa valutare le espressioni trigonometriche O rappresentare graficamente le funzioni trigonometriche generalmente.