Comment utiliser cette calculatrice de test t pour un échantillon unique ?

En savoir plus sur le Test T pour une moyenne afin que vous puissiez mieux interpréter les résultats obtenus par ce solveur : Un test t pour une moyenne est un test d'hypothèse qui tente de faire une affirmation sur la moyenne de la population (\(\sigma\)). Ce test t, contrairement au test z, ne nécessite pas de connaître l'écart-type de la population \(\sigma\).

Comment effectuer un test t pour la moyenne d'une population ?

Le test comporte deux hypothèses complémentaires, l'hypothèse nulle et l'hypothèse alternative. L'hypothèse nulle est une déclaration concernant la moyenne de la population, sous l'hypothèse de l'absence d'effet, et l'hypothèse alternative est l'hypothèse complémentaire de l'hypothèse nulle. Les principales propriétés d'un test t à un échantillon pour une moyenne de population sont les suivantes :

• Pour un test t pour une moyenne, la distribution d'échantillonnage utilisée pour la statistique du test t (qui est la distribution de la statistique du test en supposant que l'hypothèse nulle est vraie) correspond à la distribution t, avec n-1 degrés de liberté (au lieu d'être la distribution normale standard, comme dans le cas d'un test z pour une moyenne)


• En fonction de nos connaissances sur la situation "sans effet", le test t peut être bilatéral, unilatéral à gauche ou unilatéral à droite


• Le principe de base des tests d'hypothèse est que l'hypothèse nulle est rejetée si la statistique de test obtenue est suffisamment improbable si l'on suppose que l'hypothèse nulle est vraie


• La valeur p est la probabilité d'obtenir des résultats de l'échantillon aussi extrêmes ou plus extrêmes que les résultats de l'échantillon obtenus, en supposant que l'hypothèse nulle est vraie


• Dans un test d'hypothèse, il existe deux types d'erreurs. L'erreur de type I se produit lorsque nous rejetons une hypothèse nulle vraie, et l'erreur de type II se produit lorsque nous ne parvenons pas à rejeter une hypothèse nulle fausse

Comment calculer la statistique t pour un échantillon ?

Quelle est donc la formule du test t pour un seul échantillon ? Dans ce cas, la formule du test t pour la statistique t est la suivante

\[t = \frac{\bar X - \mu_0}{s/\sqrt{n}}\]

L'hypothèse nulle est rejetée lorsque la statistique t se situe dans la région de rejet, qui est déterminée par le niveau de signification (\(\alpha\)), le type de queue (bilatérale, gauche ou droite) et la valeur de la statistique t. La statistique t est rejetée lorsque la statistique t se situe dans la région de rejet nombre de degrés de liberté \(df = n - 1\)

Que se passe-t-il avec le test t lorsque j'ai 2 échantillons ?

Notez qu'il s'agit d'une calculatrice de test t à un échantillon. Si vous devez comparer deux moyennes, vous devez utiliser une calculatrice de test t à un échantillon test t pour les échantillons indépendants au lieu de cela.

De la même manière, vous pouvez avoir deux échantillons, mais ils sont appariés, appariés ou répétés, auquel cas l'outil approprié à utiliser est le suivant calculatrice de test t par paires lorsque c'est le cas.

Décision pour un test t à un échantillon

Comment prendre une décision sur un test t à un échantillon ? Tout d'abord, vous devez connaître la statistique t, que nous appelons \(t_{obs}\), et les degrés de liberté df, afin de pouvoir calculer la valeur p.

Le processus de calcul de la valeur p dépend du type de queue défini. Pour un test bilatéral, la valeur p est calculée comme \(p = \Pr(|t_{df}| > |t_{obs}|)\). Ensuite, pour un test unilatéral gauche, la valeur p est calculée comme \(p = \Pr(t_{df} < t_{obs})\), et pour un test unilatéral droit, la valeur p est calculée comme \(p = \Pr(t_{df} > t_{obs})\).

Exemple de test t à un échantillon

Un vendeur dispose d'enregistrements montrant que le client moyen dépense en moyenne 80 dollars dans son magasin, mais depuis peu, il a l'impression que ce montant a augmenté. Elle prélève un échantillon aléatoire de n = 30 clients et constate que le montant moyen dépensé dans le magasin est de 85,4 dollars, avec un écart-type de 12,4 dollars. A-t-elle suffisamment de preuves pour affirmer que le montant moyen dépensé dans son magasin a augmenté de manière significative, au seuil de signification de 0,05 ?

Solution:

Les informations suivantes ont été fournies :

Hypothesized Population Mean \((\mu)\) =	\(80\)
Sample Standard Deviation \((s)\) =	\(12.4\)
Sample Size \((n)\) =	\(30\)
Sample Mean \((\bar X)\) =	\(85.4\)
Significance Level \((\alpha)\) =	\(0.05\)

(1) Hypothèses nulle et alternative

Les hypothèses nulles et alternatives suivantes doivent être testées :

\[ \begin{array}{ccl} H_0: \mu & = & 80 \\\\ \\\\ H_a: \mu & > & 80 \end{array}\]

Cela correspond à un test unilatéral, pour lequel un test t pour une moyenne, avec un écart-type de population inconnu, utilisant l'écart-type de l'échantillon, sera utilisé.

(2) Région De Rejet

Sur la base des informations fournies, le niveau de signification est \(\alpha = 0.05\) et la valeur critique pour un test unilatéral est \(t_c = 1.699\).

La région de rejet pour ce test unilatéral est \(R = \{t: t > 1.699\}\)

(3) Statistiques Des Tests

La statistique t est calculée comme suit :

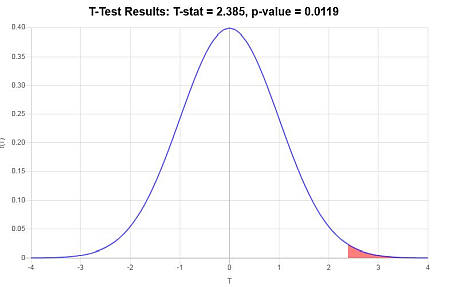
\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar X - \mu_0}{s/\sqrt{n}} \\\\ \\\\ & = & \displaystyle \frac{ 85.4 - 80}{ 12.4/\sqrt{ 30}} \\\\ \\\\ & = & 2.385 \end{array}\]

(4) Décision concernant l'hypothèse nulle

Puisqu'on observe que \(t = 2.385 > t_c = 1.699\), on en conclut que l'hypothèse nulle est rejetée.

En utilisant l'approche de la valeur P : La valeur p est \(p = 0.0119\), et puisque \(p = 0.0119 < 0.05\), on conclut que l'hypothèse nulle est rejetée.

(5) Conclusion

Il est conclu que l'hypothèse nulle Ho est rejetée. Par conséquent, il n'y a pas suffisamment de preuves pour affirmer que la moyenne de la population \(\mu\) est supérieure à 80, au niveau de signification \(\alpha = 0.05\).

Intervalle De Confiance

L'intervalle de confiance à 95 % est \(80.77 < \mu < 90.03\).

Graphiquement