Calculatrice du test z pour deux moyennes

Cette calculatrice permet d'effectuer un test z pour deux moyennes, en montrant toutes les étapes. Le test z est très similaire à un test t mais avec une différence évidente : dans le cas d'une Test Z nous devons connaître l'écart-type de la population correspondante.

Pour ce test, vous devez fournir deux échantillons, ainsi que l'écart-type de la population correspondant à chaque groupe. Vous vous demandez peut-être ce qui se passe si je n'ai pas ces écarts types de population : la réponse est simple : vous NE POUVEZ PAS effectuer le test z pour deux moyennes.

Une fois que vous avez fourni toutes les données requises, il vous suffit de cliquer sur "Calculer", et toutes les étapes du processus vous seront présentées.

Qu'est-ce qu'un test z à deux échantillons ?

Un test z à deux échantillons est un type de test z qui compare les moyennes de deux groupes. Vous pouvez fournir les données de l'échantillon (ainsi que les écarts-types de la population), ou vous pouvez exécuter un test z à deux échantillons test z pour deux moyennes avec des données résumées pour lesquels vous devez fournir les moyennes de l'échantillon au lieu des données de l'échantillon.

Le choix entre le test z pour les données d'un échantillon et le test z pour les données résumées dépend en grande partie des informations dont vous disposez.

Formule de test z pour deux moyennes

Il existe une expression simple pour la formule utilisée dans ce test. La formule du test z est

\[z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}} \]

L'avantage dans ce cas est que nous n'avons pas besoin de gérer les degrés de liberté, comme dans le cas de la méthode test t pour deux moyennes et avec les tests t en général.

Comment effectuer un test z à 2 échantillons sur cette calculatrice ?

• Étape 1 : Identifiez les échantillons que vous souhaitez comparer. En général, vous souhaiterez effectuer une analyse statistique descriptive pour vous assurer que les échantillons sont raisonnablement en forme de cloche
• Étape 2 : Vous devez également identifier les écarts types de la population \(\sigma_1\) et \(\sigma_2\). Si vous ne les avez pas, vous ne pouvez pas effectuer de test z
• Étape 3 : A partir des échantillons, vous devez trouver les moyennes de l'échantillon \(\bar X_1\) et \(\bar X_2\)
• Étape 4 : Il ne vous reste plus qu'à introduire vos informations dans la formule \(z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}}\)
• Étape 5 : Une fois que vous avez la statistique z, que vous appelez \(z_{obs}\), vous devez calculer la valeur p
• Étape 6 : Pour les tests unilatéraux, vous calculez \(p = \Pr(Z < z_{obs})\). Pour les tests unilatéraux à droite, vous calculez \(p = \Pr(Z > z_{obs})\) et pour les tests bilatéraux, vous calculez \(p = \Pr(|Z| > z_{obs})\)
• Étape 7 : Une fois que vous avez la valeur p, vous tirez une conclusion basée sur la valeur choisie du niveau de signification \(\alpha\) : si \(p < \alpha\), vous rejetez l'hypothèse nulle, et dans le cas contraire, vous n'avez pas assez de preuves pour rejeter l'hypothèse nulle

Un point important : si vous ne rejetez pas l'hypothèse nulle Ho, cela ne signifie pas que vous acceptez l'hypothèse nulle, mais simplement que vous n'avez pas pu trouver suffisamment de preuves pour la rejeter.

Quelle est la différence avec le test z pour deux proportions ?

Ils sont similaires en ce sens qu'il s'agit dans les deux cas de tests z, qui utilisent la formule distribution normale pour déterminer toutes les probabilités associées.

La différence réside dans le fait qu'ils mesurent des choses différentes : Le test z pour deux moyennes compare les moyennes de deux groupes, lorsque ces variables sont mesurées au niveau de l'intervalle ou du ratio, tandis que le test z pour deux proportions compare la proportion d'une certaine caractéristique associée aux données.

Comment effectuer un test z à deux échantillons dans excel ?

Excel possède des fonctions internes qui vous permettent d'effectuer un test z et de nombreuses autres procédures, mais il ne vous montre pas toutes les étapes du processus comme le fait cette calculatrice.

En fin de compte, vous pourrez peut-être obtenir une réponse numérique à partir d'Excel ou d'une autre calculatrice, mais vous ne saurez pas comment trouver le test z sur une calculatrice ordinaire.

Exemple de test z à deux moyennes

Une instructrice teste une méthode d'enseignement et fait suivre une méthode à un échantillon de 10 élèves et l'autre méthode à un échantillon de 11 élèves. Les notes obtenues après avoir enseigné selon ces méthodes sont les suivantes :

Groupe 1 : 89, 78, 90, 100, 90, 92, 90, 80, 89, 93

Groupe 2 : 91, 89, 91, 95, 92, 93, 91, 87, 90, 94, 90

Elle sait également que l'écart-type des notes pour la première méthode est de 3,4, alors qu'il est de 4,1 pour la seconde. L'instructeur peut-il conclure qu'il existe une différence significative entre les méthodes ? Utiliser un seuil de signification de 0,05

Solution :

Les informations suivantes ont été fournies à titre d'exemple :

Échantillon 1	Échantillon 2
89	91
78	89
90	91
100	95
90	92
92	93
90	91
80	87
89	90
93	94
	90

Pour réaliser un test z sur deux échantillons indépendants, nous devons calculer les statistiques descriptives des échantillons :

	Échantillon 1	Échantillon 2
	89	91
	78	89
	90	91
	100	95
	90	92
	92	93
	90	91
	80	87
	89	90
	93	94
		90
Moyenne	89.1	91.1818
n	10	11

En résumé, les statistiques descriptives suivantes seront utilisées pour le calcul de la statistique z :

Les informations suivantes ont été fournies :

Sample Mean 1 \((\bar X_1)\) =	\(89.1\)
Population Standard Deviation 1\((\sigma_1)\) =	\(3.4\)
Sample Size 1\((n_1)\) =	\(10\)
Sample Mean 2 \((\bar X_2)\) =	\(91.1818\)
Population Standard Deviation 2 \((\sigma_2)\) =	\(4.1\)
Sample Size 2\((n_2)\) =	\(11\)
Significance Level \((\alpha)\)	\(0.05\)

(1) Hypothèses nulle et alternative

Les hypothèses nulles et alternatives suivantes doivent être testées :

\[ \begin{array}{ccl} H_0: \mu_1 & = & \mu_2 \\\\ \\\\ H_a: \mu_1 & \ne & \mu_2 \end{array}\]

Cela correspond à un test bilatéral, et un test z pour deux moyennes, avec des écarts types de population connus, sera utilisé.

(2) Région De Rejet

Sur la base des informations fournies, le niveau de signification est \(\alpha = 0.05\), et la valeur critique pour un test bilatéral est \(z_c = 1.96\).

La région de rejet pour ce test bilatéral est \(R = \{z: |z| > 1.96\}\)

(3) Statistiques Des Tests

La statistique z est calculée comme suit :

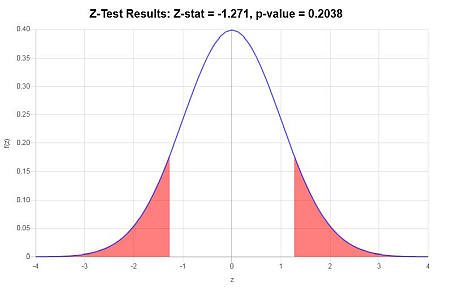
\[ \begin{array}{ccl} z & = & \displaystyle \frac{\bar X_1 - \bar X_2}{\sqrt{ {\sigma_1^2/n_1} + {\sigma_2^2/n_2} }} \\\\ \\\\ & = & \displaystyle \frac{ 89.1 - 91.1818}{\sqrt{ {3.4^2/10} + {4.1^2/11} }} \\\\ \\\\ & = & -1.271 \end{array}\]

(4) Décision concernant l'hypothèse nulle

Puisqu'il est observé que \(|z| = 1.271 \le z_c = 1.96\), il est alors conclu que l'hypothèse nulle n'est pas rejetée.

En utilisant l'approche de la valeur P : La valeur p est \(p = 0.2038\), et puisque \(p = 0.2038 \ge 0.05\), on conclut que l'hypothèse nulle n'est pas rejetée.

(5) Conclusion

Il est conclu que l'hypothèse nulle Ho n'est pas rejetée. Par conséquent, il n'y a pas suffisamment de preuves pour affirmer que la moyenne de la population \(\mu_1\) est différente de \(\mu_2\), au niveau de signification \(\alpha = 0.05\).

Intervalle De Confiance

L'intervalle de confiance à 95% pour \(\mu_1-\mu_2\) est \(-5.293 < \mu_1 - \mu_2 < 1.129\).

Graphiquement

Plus de calculateurs de tests statistiques

En étroite relation avec cette calculatrice, vous avez la calculatrice pour un test z pour deux échantillons avec des données résumées qui effectue fondamentalement la même procédure, mais reçoit le résumé des statistiques descriptives déjà connues.

Dans la famille des tests avec nous avons le test z pour une moyenne, et le test z pour une moyenne, et le test z pour une moyenne Test Z pour deux proportions .

Aussi, vous pourriez être intéressé par un calculatrice de fractions mixtes selon le contexte d'apprentissage, les nombres mixtes sont traités comme des entités importantes. Dans les environnements plus élémentaires, les nombres mixtes sont traités comme des entités importantes, tandis que dans les environnements plus avancés, les nombres mixtes sont simplement présentés dans leur notation fractionnaire.