Comment calculer les résidus de régression ?

Les résidus de régression correspondent à la différence entre les valeurs observées (\(y\)) et les valeurs prédites correspondantes (\(\hat y\)).

Équation résiduelle de régression

Lors d'une analyse de régression linéaire, la première étape consiste à faire un nuage de points des données X et Y dont vous disposez, et si vous observez un modèle linéaire relativement étroit, vous pouvez alors valablement effectuer l'analyse linéaire

Rappelons que si \(\hat \beta_0\) et \(\hat \beta_1\) sont respectivement l'ordonnée à l'origine et la pente estimées correspondantes, la valeur prédite (\(\hat y\)) pour une valeur donnée \(x\) est la suivante

\[ \hat y = \hat \beta_0 + \hat \beta_1 x \]

Ensuite, le résidu associé à la paire \((x,y)\) est défini à l'aide de l'équation statistique résiduelle suivante :

\[ \text{Residual} = y - \hat y \]

Le résidu représente la distance entre la prédiction et la valeur réelle observée. Cela signifie que nous aimerions avoir des résidus aussi petits que possible.

En effet, l'idée des moindres carrés Régression linéaire est de trouver les paramètres de régression basés sur ceux qui minimiseront la somme des carrés des résidus.

Comment trouver les résidus d'une régression ?

• Collecter les données de l'échantillon pour X et Y
• Effectuez une analyse de régression linéaire et trouvez l'équation de régression \(\hat y = \hat \beta_0 + \hat \beta_1 x\)
• Pour chaque point d'échantillonnage \(x_i\) et \(y_i\), vous calculez le résidu à l'aide de la formule : \(\text{Residual} = y_i - \hat y_i \)
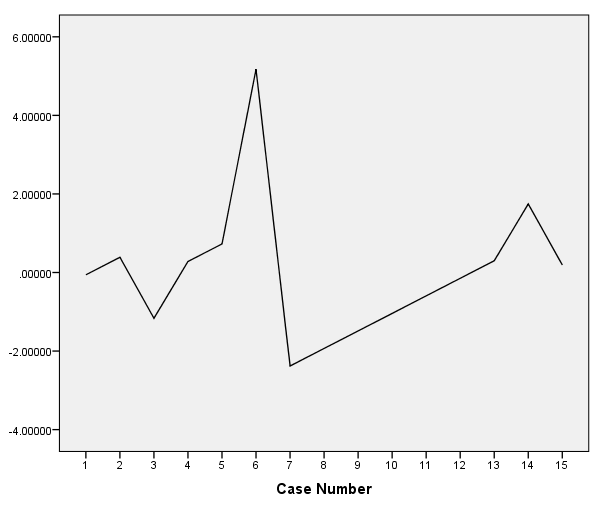
• Une fois que vous disposez de tous les points résiduels, vous pouvez les représenter de différentes manières pour évaluer la qualité et les propriétés du modèle estimé
• Le calcul des résidus est important car il permet d'évaluer graphiquement la plausibilité des hypothèses de régression.
• Pour que les résultats de la régression soient fiables, on s'attend à ce que les résidus aient au moins un distribution de probabilité normale .

Que fait cette calculatrice de résidus ?

Cette calculatrice de résidus prend les données que vous avez fournies pour X et Y et calcule le modèle de régression linéaire, étape par étape.

Ensuite, pour chaque valeur des données de l'échantillon, la valeur prédite correspondante est calculée, et cette valeur est soustraite des valeurs observées y, pour obtenir les résidus.

Tous ces éléments seront mis sous forme de tableaux et vous seront présentés de manière claire. En outre, un nuage de points des résidus en fonction de l'indice de masse corporelle (IMC) sera présenté valeurs prédites sera présenté. Ce diagramme des résidus est essentiel pour évaluer si les hypothèses du modèle de régression linéaire sont respectées ou non.

Que pouvez-vous faire d'autre avec ces données ?

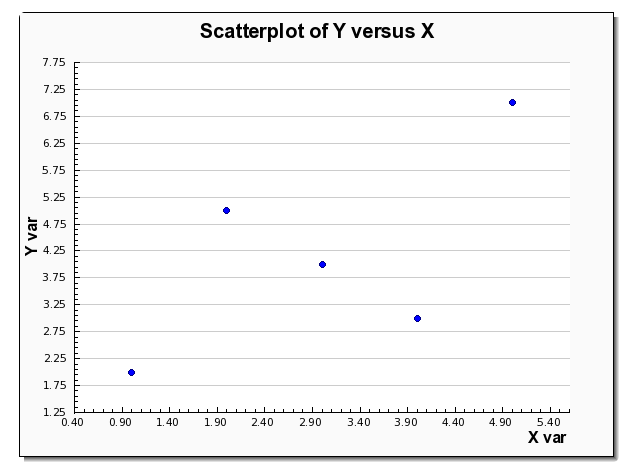
En général, la première étape d'une analyse de régression linéaire consiste à effectuer une analyse corrélationnelle. Vous pouvez utiliser notre calculateur de coefficient de corrélation pour trouver le coefficient de corrélation, qui indique le degré d'association entre les deux variables.

Le calcul du coefficient de corrélation s'accompagne généralement de la construction d'un diagramme de dispersion. En utilisant un diagramme de dispersion et le coefficient de corrélation, nous pouvons décider s'il est approprié ou non d'effectuer une analyse de régression linéaire, en particulier si nous avons découvert à l'aide de ce diagramme de dispersion qu'il n'y a pas de corrélation entre les données coefficient de corrélation calculateur de signification que la corrélation est significativement différente de zéro.