Graphique de tracé résiduel
Instructions: Utilisez ce graphique de tracé résiduel pour construire un tracé résiduel pour la valeur obtenue avec une analyse de régression linéaire basée sur les données d'échantillon que vous avez fournies. Veuillez saisir les données de la variable indépendante \((X)\) et de la variable dépendante (\(Y\)), sous la forme ci-dessous:
A propos de ce graphique de tracé résiduel
L'une des principales conditions pour que les résultats et les prévisions d'une analyse de régression soient valides est que les hypothèses de régression linéaire soient satisfaites. Les hypothèses d'indépendance, de normalité et d'homoscédasticité des erreurs sont essentielles pour obtenir des résultats de régression fiables
L'utilisation de graphiques basés sur les résidus est cruciale pour évaluer rapidement si les hypothèses ne sont pas satisfaites ou non et si une correction est nécessaire.
Une fois que nous avons estimé les coefficients de régression correspondant à l'ordonnée à l'origine et à la pente, \(\hat \beta_0\) et \(\hat \beta_1\), nous pouvons procéder au calcul des valeurs prédites.
Comment calculez-vous les valeurs résiduelles de régression?
Le calcul est simple. La première étape consiste à calculer les coefficients de régression linéaire, qui sont utilisés de la manière suivante pour calculer les valeurs prédites:
\[ \hat y = \hat \beta_0 + \hat \beta_1 x \]Une fois les valeurs prédites \(\hat y\) calculées, nous pouvons calculer les résidus comme suit:
\[\text{Residual} = y - \hat y\]Que vous montre un graphique résiduel?
Des graphiques résiduels sont utilisés pour vérifier les hypothèses de régression linéaire. C'est un moyen visuel d'évaluer rapidement si les hypothèses sont gravement violées ou non. Pour une évaluation plus concise de la réalisation des hypothèses de régression linéaire, il existe un test statistique spécifique pour chaque hypothèse.
Les différents types de tracés résiduels sont: les résidus par rapport au nombre d'observation (fourni par ce calculateur), qui est utilisé pour évaluer l'hypothèse d'indépendance de l'erreur. De plus, nous avons le tracé de normalité des résidus (qui est utilisé pour évaluer la normalité des erreurs) et le tracé des résidus par rapport aux valeurs prédites, qui est utilisé pour évaluer l'hypothèse d'homoscédasticité de l'erreur.
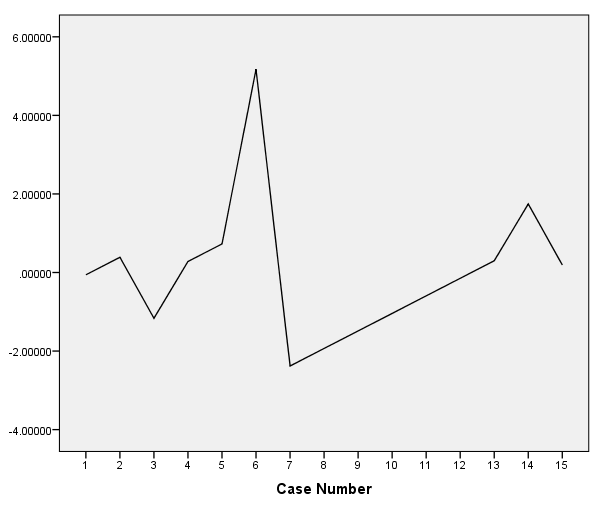
Comment représenter graphiquement les résidus d'un modèle de régression linéaire?
Il existe différents types de parcelles impliquant des résidus. Cette calculatrice vous montrera le calcul des résidus et vous montrera un graphique des résidus en fonction du nombre d'observation.
Ce créateur de tracé résiduel vous permet d'évaluer si les résidus semblent ou non apparaître au hasard dans le temps (ils sont donc indépendants), ou s'il existe une sorte de modèle dans le temps (ce qui indiquerait que les résidus ne seraient pas indépendants, et un l'hypothèse de régression serait violée).
Si vous avez seulement besoin de calculer les résultats de la régression, vous pouvez utiliser ceci calculatrice de modèle de régression linéaire , afin d'obtenir les coefficients de régression estimés sur la base des données d'échantillon fournies.
