Calculateur de coefficient de corrélation

Le coefficient de corrélation calculé ci-dessus correspond au coefficient de corrélation de Pearson. Pour le calculer, il faut que les deux variables X et Y soient mesurées au moins au niveau de l'intervalle (ce qui signifie qu'il ne fonctionne pas avec des variables nominales ou ordinales).

La formule du coefficient de corrélation de Pearson est la suivante :

\[r =\frac{n \sum_{i=1}^n x_i y_i - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \sqrt{n \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n y_i \right)^2} }\]

ou de manière équivalente

\[r = \frac{\sum_{i=1}^n x_i y_i - \frac{1}{n}\left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{\sum_{i=1}^n x_i^2 - \frac{1}{n}\left( \sum_{i=1}^n x_i \right)^2} \sqrt{\sum_{i=1}^n y_i^2 - \frac{1}{n}\left( \sum_{i=1}^n y_i \right)^2}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]

Si vous avez deux variables ou plus, vous pouvez utiliser la fonction calculateur de matrice de corrélation . En outre, si les données relatives aux variables \(X\) et \(Y\) ne répondent pas aux hypothèses paramétriques de la corrélation de Pearson, vous devez utiliser la méthode suivante Calculateur de corrélation de Spearman au lieu de cela.

Corrélation et régression

La corrélation et la régression ne sont pas la même chose, bien qu'il s'agisse de concepts étroitement liés. L'analyse de corrélation correspond au calcul du coefficient de corrélation, qui est une valeur comprise entre -1 et 1, permettant d'évaluer le degré d'association linéaire entre deux variables.

Plus la valeur absolue de la corrélation est proche de 1, plus l'association linéaire entre les deux variables est étroite. Une valeur proche de 1 indique une association linéaire positive étroite, et une valeur proche de -1 indique une association négative étroite

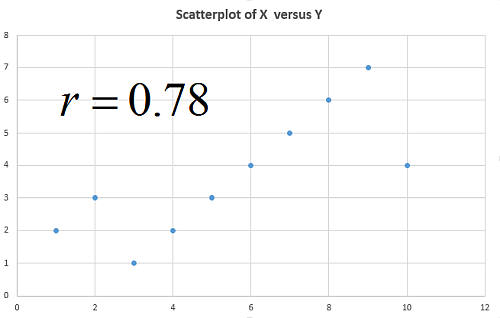
Le processus de réalisation d'une analyse de corrélation implique souvent aussi construction d'un nuage de points afin de confirmer l'information donnée par le coefficient.

Une fois que nous avons confirmé que la corrélation est proche de 1 en valeur absolue et que le nuage de points présente un modèle linéaire raisonnablement serré, nous pouvons exécuter un test de corrélation Régression linéaire afin d'évaluer quantitativement l'effet de la variable indépendante X sur la variable dépendante Y.

Puis-je utiliser les scores z pour calculer le coefficient de corrélation ?

Certainement ! Vous avez vu des z-scores partout dans les statistiques et naturellement, vous vous demandez si vous pouvez.. calculer la corrélation avec les scores z . C'est tout à fait possible, et c'est d'ailleurs la façon habituelle de procéder dans les statistiques des sciences sociales.

Autres calculatrices similaires à cette calculatrice de corrélation

Il y a aussi le concept de multiple correlation coefficient lorsque vous avez plus d'un prédicteur, qui est obtenue en calculant la corrélation entre les valeurs observées \(Y\) et les valeurs prédites \(\hat Y\) par la régression.