En savoir plus sur cette calculatrice graphique

Utilisez cette calculatrice graphique pour tracer le graphique d'une fonction que vous fournissez. Vous pouvez tracer une fonction simple comme f(x) = x^2, ou une fonction plus complexe comme f(x) = tan(x)/x. Cette calculatrice tentera de simplifier l'expression avant de la représenter graphiquement.

Une fois qu'une fonction valide est fournie, il vous suffit de cliquer sur le bouton "Graphique", et vous obtiendrez le graphique en ligne, ainsi que toutes les simplifications pertinentes, le cas échéant.

Remarquez qu'un valide est nécessaire pour que le système sache sans ambiguïté quelle est la fonction que vous avez l'intention de représenter graphiquement. Par exemple, quelque chose comme (sin(x))/x est valable, mais quelque chose comme sin x / x est ambigu, et le système essaiera de l'analyser d'une manière que vous n'avez peut-être pas voulue.

Comment faire pour représenter graphiquement les fonctions ?

La représentation graphique peut être très simple lorsque les fonctions sont simples. L'idée est simplement d'identifier les paires (x, y) = (x, f(x)) et de trouver le cadre de fenêtre approprié pour les afficher.

Le Présent calculatrice graphique en ligne vous facilitera la tâche en déterminant les points pertinents à représenter graphiquement et en choisissant la bonne fenêtre à afficher.

Étapes de la représentation graphique d'une fonction

• Étape 1 : Identifiez clairement la fonction que vous voulez tracer et procédez à toute simplification évidente. Par exemple, si la fonction contient quelque part \(\sin^2(x) + \cos^2(x)\), vous devez observer que \(\sin^2(x) + \cos^2(x) = 1\) et ensuite simplifier dans votre expression.
• Étape 2 : Une fois que toutes les simplifications évidentes ont été effectuées, vous devez décider d'un intervalle pour les valeurs x. Il n'y a pas de règles fixes pour cela, mais vous devez généralement prendre en compte tous les points importants, comme les discontinuités, les asymptotes verticales, etc.
• Étape 3 : Une fois que la plage des valeurs x est déterminée, vous devez vous faire une idée de la plage des valeurs y, de manière à ce qu'aucun point du graphique ne soit hors du cadre.

L'idée d'établir un graphique est donc simple, mais vous devez encore décider de certaines choses si vous faites les choses manuellement. L'utilisation d'un outil graphique éliminera définitivement toute incertitude.

Pourquoi dois-je tracer un graphique de la fonction

Le graphique fourni par cette calculatrice graphique en ligne vous permettra d'obtenir une très bonne représentation du comportement de la fonction. Traverse-t-elle l'axe des x ou des y, présente-t-elle des points de maximum ou de minimum localisés ? Vous pouvez obtenir beaucoup d'informations pertinentes sur la fonction en regardant simplement le graphique.

Vous ne connaîtrez pas nécessairement les intercepts ou les extrema exacts en regardant simplement le graphique, mais vous aurez une assez bonne idée de l'endroit où les trouver, s'ils existent.

Avantages de l'utilisation d'un outil graphique

Comme nous l'avons dit, il n'est pas trop difficile de faire un graphique, mais il y a des détails à régler, en particulier ceux qui déterminent le cadre de la fenêtre qui sera affichée.

Cela signifie que vous pouvez avoir un graphique "correct" pour une fonction, mais qui affiche une partie du graphique qui n'est pas la plus pertinente, et vous pouvez manquer la plupart des parties importantes de la fonction, qu'il serait bon d'afficher. Un bon concepteur de graphiques s'en chargera pour vous.

Exemple : calculer le graphique d'une fonction

Trouvez le graphique de la fonction : \(f(x) = \displaystyle \frac{\sin x}{x}\)

Solution : La fonction suivante a été fournie : \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), pour laquelle nous devons construire son graphe.

Remarquez que la fonction n'est pas définie à \(x = 0\), bien qu'elle ait une discontinuité réparable, puisque

\[\lim_{x\to 0} \frac{\sin x}{x} = 1\]

Le graphique suivant est obtenu pour la fonction donnée sur l'intervalle \([-5, 5]\) :

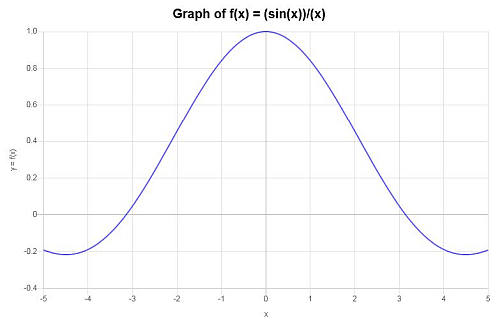
qui conclut le calcul.

Plus de calculatrices graphiques en ligne

Bien que cette Graphiqueur est générique dans le sens où il peut représenter n'importe quel type de fonction, vous pouvez également utiliser un type de graphique spécialisé pour des fonctions spécifiques, qui peut vous donner plus d'informations sur la base de la structure de la fonction.

Par exemple, vous pouvez utiliser calculatrice de graphiques linéaires qui est spécialement conçu pour tracer des courbes. Ou, si vous avez affaire à une fonction trigonométrique, vous pouvez utiliser ceci calculatrice de trigonométrie qui tentera également de trouver des paramètres spécifiques des fonctions trigonométriques, notamment l'amplitude, la période, la fréquence, etc.

Ou vous pouvez utiliser ceci Graphique polynomial lorsqu'il s'agit de polynômes.

Vous pouvez également utiliser ce Calculatrice de fonction exponentielle l'objectif est de trouver les paramètres d'une fonction exponentielle à partir de deux points de passage de la courbe.