En savoir plus sur la matrice de corrélation

Une matrice de corrélation est un tableau dans lequel les corrélations par paire entre plusieurs variables sont organisées de manière pratique sous forme de matrice. La valeur de la ième ligne et de la jième colonne correspond à la corrélation entre les variables \(X_i\) et \(X_j\).

En d'autres termes, la matrice de corrélation est un résumé de toutes les corrélations qui peuvent être trouvées pour un ensemble de variables, pour lesquelles des données d'échantillon sont disponibles.

Le calcul de la corrélation est crucial, car il s'agit de l'étape précédente nécessaire pour appliquer une méthode d'évaluation de l'impact sur l'environnement Calculateur de régression linéaire pour trouver le modèle des moindres carrés. Mais cela ne doit être tenté que lorsque le la corrélation est significative .

Formule de la matrice de corrélation

Puisque \(corr(X_i, X_j) = corr(X_j, X_i)\), la matrice de corrélation est symétrique, et pour cette raison, afin de ne pas être redondante, la matrice de corrélation ne rapporte que les valeurs à partir de la diagonale et vers le haut. Pour d'autres opérations de corrélation, vous pouvez calculer un coefficient de corrélation montrant toutes les étapes, ou vous pouvez utiliser ceci calculateur de corrélation critique .

Comment calculer une matrice de corrélation ?

Pour comprendre comment calculer une matrice de corrélation, il faut d'abord savoir comment calculer la corrélation de Pearson, car la matrice de corrélation est simplement la matrice des corrélations entre toutes les paires de variables possibles.

Afin de procéder au calcul de la matrice de corrélation, vous devez suivre les étapes suivantes :

Étape 1 : Dressez la liste des variables que vous avez, par exemple X1, X2, ..., etc. Chacune de ces variables est associée à un échantillon

Étape 2 : Prenez la ième et la jième variables de votre liste, Xi et Xj, et calculez leur coefficient de corrélation. Appelez-le \(r_{ij}\)

Étape 3 : Prenez la valeur \(r_{ij}\) et vous obtiendrez la valeur de la ligne i, colonne j de la matrice de corrélation

Les valeurs de corrélation proches de 1 ou de -1 indiquent des associations linéaires fortes, ce qui suggère qu'un Calculateur de régression linéaire (ou un régression linéaire multiple en fonction du nombre de prédicteurs).

Comment utilise-t-on une matrice de corrélation ?

Il s'agit d'un point qu'il convient d'aborder, car une matrice de corrélation peut souvent être présentée sous différents formats. La matrice de corrélation sera un tableau avec le même nombre de lignes et de colonnes, où le nom des variables apparaîtra dans les lignes et les colonnes correspondantes.

Ainsi, si la première variable est \(X_1\), la première ligne vous donnera le coefficient de corrélation de \(X_1\) et de chacune des autres variables. Et si la deuxième variable est \(X_2\), alors la deuxième ligne vous donnera le coefficient de corrélation de \(X_2\) et de chacune des autres variables, et ainsi de suite.

En se basant sur la façon dont cela est défini, dans la ligne 1, colonne 1, vous avez la corrélation de \(X_1\) avec elle-même, qui est de 1, puis dans la ligne 2, colonne 2, vous avez la corrélation de \(X_2\) avec elle-même, qui est également de 1, et ainsi de suite.

Vous constaterez donc que la diagonale de la matrice de corrélation ne contient toujours que des 1. Puisque c'est quelque chose qui se produit toujours, la matrice de corrélation calculée omettra souvent la diagonale (parce que nous savons déjà qu'elle contient des 1, alors quel est l'intérêt de l'écrire explicitement).

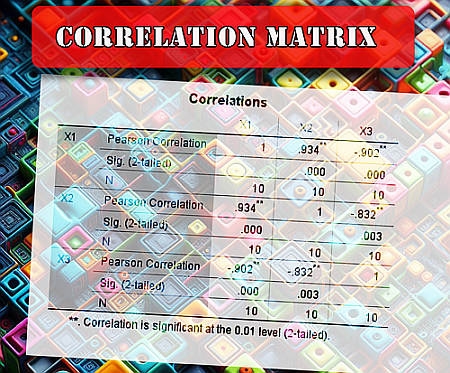
Mais il y a une autre chose à observer : la corrélation entre \(X_1\) et \(X_2\) est la même que la corrélation entre \(X_2\) et \(X_1\), de sorte que la matrice de corrélation est la suivante symétrique les valeurs situées sous la diagonale reflètent donc les valeurs situées au-dessus de la diagonale.

C'est pourquoi vous voyez très souvent une matrice de corrélation avec des valeurs rapportées uniquement au-dessus de la diagonale (ou en dessous), parce que nous savons que la diagonale est égale à 1 et que nous savons que les valeurs en dessous de la diagonale sont le reflet des valeurs au-dessus de la diagonale.