Más información sobre este creador de gráficos P.

Esta calculadora de la carta P es una herramienta gráfica muy utilizada para evaluar si un proceso está en control estadístico, normalmente analizando el comportamiento de la proporción de defectos en muchas muestras.

La gran ventaja de utilizar una herramienta gráfica es que se pueden encontrar fácilmente patrones e identificar puntos que parecen desviarse de un comportamiento "normal", o más precisamente, de lo que se esperaría bajo ciertos supuestos comunes de distribución.

¿Cómo puedo utilizar la calculadora de la carta P en línea?

La idea es que usted tiene una lista de muestras \(N\), y para cada muestra tiene un número de defectos y el tamaño de la muestra. Normalmente, el tamaño de la muestra es el mismo para todas las muestras, pero no siempre es así.

A continuación, para cada muestra se calculará la proporción muestral de defectuosos \(\p_i\). En total, tendremos \(N\) proporción muestral de defectuosos, una para cada muestra. Por último, encontrará la media de la proporción de defectuosos, que llamará \(\bar{p}\).

Después de tener todo eso, puede utilizar las siguientes fórmulas para obtener los límites de control inferior y superior para el gráfico p

\[ LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \] \[ UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \]

donde \(k\) es el tamaño de muestra común de TODAS las muestras con las que se trabaja.

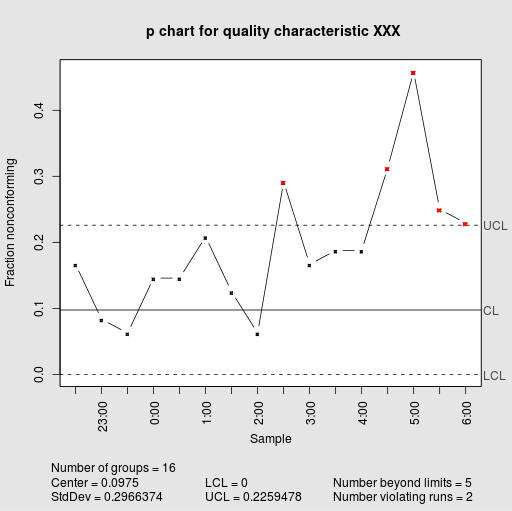
Resumiendo: ¿Cómo se hace un gráfico P?

Paso 1. Lo primero que hay que hacer es recoger los datos que se quieren medir, en este caso, los defectuosos, ya que lo que interesa es analizar la proporción de defectuosos en última instancia.

Paso 2. Ahora, para cada muestra se calcula la proporción muestral de defectuosos (es decir, el número de defectuosos dividido por el tamaño de la muestra).

Paso 3. El siguiente paso es calcular la media de toda la proporción de defectos de la muestra.

Paso 4. A continuación, debe utilizar las fórmulas para los límites de control inferior y superior \(LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}}\) y \(UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \).

Paso 5. Ahora se construye un gráfico en el que se traza la proporción de defectuosos para cada muestra, en forma de gráfico de líneas, y también hay que trazar los límites inferior y superior, así como la línea central.

Paso 6. En el último paso, se determina si alguna proporción de defectos supera alguno de los límites de control.

Aquellos puntos que sobrepasan los límites de control inferior y superior, si los hay, se dice que están fuera de control estadístico, y también que el proceso no está en control estadístico. Cuando no hay puntos fuera de control estadístico, entonces decimos que el proceso está en control estadístico.

Otro gráfico de control

Tal vez le interese utilizar un Gráfico R para evaluar si la variabilidad del proceso está controlada o no. Además, si necesita evaluar si el centro del proceso está en control estadístico, puede utilizar este Creador de gráficos de barras X .