Deskriptive Statistik üben
Der beste Weg, um zu lernen, wie man Probleme mit der beschreibenden Statistik richtig löst, ist die PRAXIS. Hier finden Sie einige Schritt-für-Schritt-Beispiele, exklusiv für unsere Abonnenten
Frage 1: HiEd hat in diesem Jahr bisher 5 Rekrutierungsbesuche in der Region durchgeführt. Die Anzahl der Abiturienten, die an diesen Veranstaltungen teilnehmen, ist unten angegeben.
10 15 20 35 20
Die durchschnittliche Anzahl der Abiturienten, die an einer Veranstaltung teilnehmen, beträgt 20.
ein. Bestimmen Sie den Bereich für diese Probe.
b. Bestimmen Sie die Standardabweichung.
Lösung: (a) Der Bereich wird berechnet als:
\[Range=Max-Min = {35}-{10} = {25}\]
(b) Schließlich zeigt die folgende Tabelle die erforderlichen Berechnungen, die zur Berechnung der Standardabweichung erforderlich sind:
|
X. |
X² |
|
|
10 |
100 |
|
|
fünfzehn |
225 |
|
|
20 |
400 |
|
|
35 |
1225 |
|
|
20 |
400 |
|
|
Summe = |
100 |
2350 |
Die Stichprobenvarianz beträgt
\[{{s}^{2}}=\frac{1}{n-1}\left( \sum{X_{i}^{2}}-\frac{{{\left( \sum{{{X}_{i}}} \right)}^{2}}}{n} \right)=\frac{1}{5-1}\left( 2350-\frac{{{\left( 100 \right)}^{2}}}{5} \right)=87.5\]und auch wir finden, dass die Standardabweichung wird berechnet als
\[s=\sqrt{87.5}=9.3541\]
,p> Question 2: The Financial Times/Harris poll is a monthly online poll of adults from six countries in Europe and the united states. The poll conducted in January 2008 included 1015 adults. One of the questions asked was "How would you rate the federal bank in handling the credit problems in the financial markets?" Possible responses were excellent, good, fair, bad, and terrible. The 1015 responses for this question can be found in the data file named fedbank.ein. Konstruieren Sie eine Häufigkeitsverteilung.
b. Konstruieren Sie eine prozentuale Häufigkeitsverteilung.
c. Erstellen Sie ein Balkendiagramm für die prozentuale Häufigkeitsverteilung.
d. Kommentar dazu, wie Erwachsene in den USA glauben, dass die Bundesbank mit den Kreditproblemen auf den Finanzmärkten umgeht.
e. In Spanien wurden 1114 Erwachsene gefragt: „Wie würden Sie die europäische Zentralbank bei der Bewältigung der Kreditprobleme an den Finanzmärkten bewerten?“ Die prozentuale Häufigkeitsverteilung lautet wie folgt.
Rating Prozent Häufigkeit
ausgezeichnet 0
gut 4
Messe 46
schlecht 40
schrecklich 10
Vergleichen Sie die in Spanien erzielten Ergebnisse mit den in den USA erzielten Ergebnissen.
Lösung: (a) Folgendes wird erhalten:
|
Bewertung |
Frequenz |
|
Schlecht |
244 |
|
Ausgezeichnet |
20 |
|
Messe |
528 |
|
Gut |
101 |
|
Schrecklich |
122 |
|
Gesamtsumme |
1015 |
(b) Jetzt bekommen wir:
|
Bewertung |
Frequenz |
Prozentuale Häufigkeit |
|
Schlecht |
244 |
24,04% |
|
Ausgezeichnet |
20 |
1,97% |
|
Messe |
528 |
52,02% |
|
Gut |
101 |
9,95% |
|
Schrecklich |
122 |
12,02% |
|
Gesamtsumme |
1015 |
100,00% |
(c) Folgendes wird erhalten:
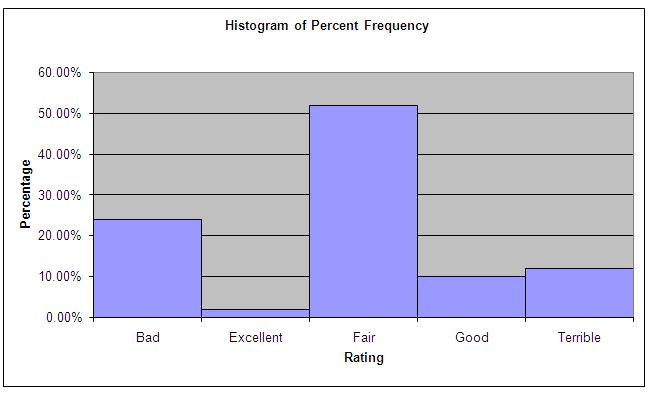
(d) In der großen Mehrheit glauben US-Erwachsene, dass die Fed fair damit umgeht.
(e) In Spanien denken die meisten Erwachsenen, dass der Umgang fair und schlecht ist.
Frage 3: Für die folgenden Punktzahlen:
3, 7, 6, 5, 5, 9, 6, 4, 6, 8, 10, 2, 7, 4, 9, 5, 6, 3, 8
ein. Erstellen Sie eine Häufigkeitsverteilungstabelle.
b. Skizzieren Sie ein Polygon mit der Verteilung.
c. Beschreiben Sie die Verteilung anhand der folgenden Merkmale:
(1) Wie ist die Form der Verteilung?
(2) Welche Punktzahl identifiziert das Zentrum (den Durchschnitt) für die Verteilung am besten?
(3) Sind die Punktzahlen zusammengefasst oder über die Skala verteilt?
Lösung: (a) Die aus den bereitgestellten Daten erhaltenen Mindest- und Höchstwerte sind
Min = 2
Max = 10
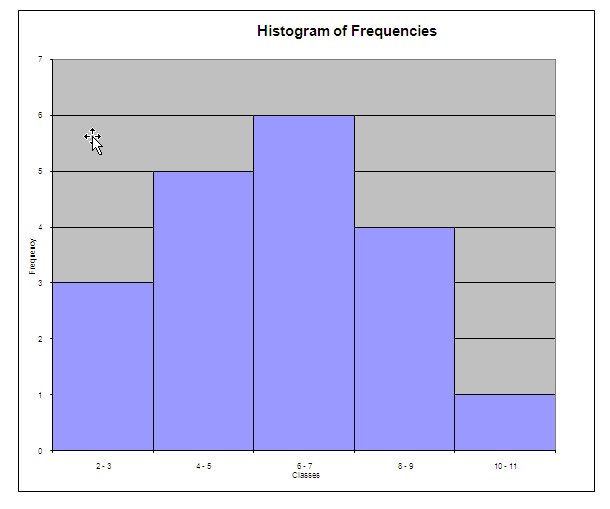
Basierend darauf wählen wir die niedrigste Klasse als 2. Die minimale Klassenbreite ist (10 - 2) / 5 = 1,6, also wählen wir eine Klassenbreite von 2. Daher werden die jeweiligen unteren Klassengrenzen als Li = 2 berechnet + 2 * i. Die folgende Tabelle zeigt die Häufigkeitstabelle:
|
Klassen |
Frequenz |
Rel. Frequenz |
Kumulative Häufigkeit |
Rel. Kumulative Häufigkeit |
|
2 - 3 |
3 |
0,158 |
3 |
0,158 |
|
4 - 5 |
5 |
0,263 |
8 |
0,421 |
|
6 - 7 |
6 |
0,316 |
14 |
0,737 |
|
8 - 9 |
4 |
0,211 |
18 |
0,947 |
|
10 - 11 |
1 |
0,053 |
19 |
1 |
Das folgende Histogramm wird erhalten
(b) Das folgende Frequenzpolygon wird erhalten
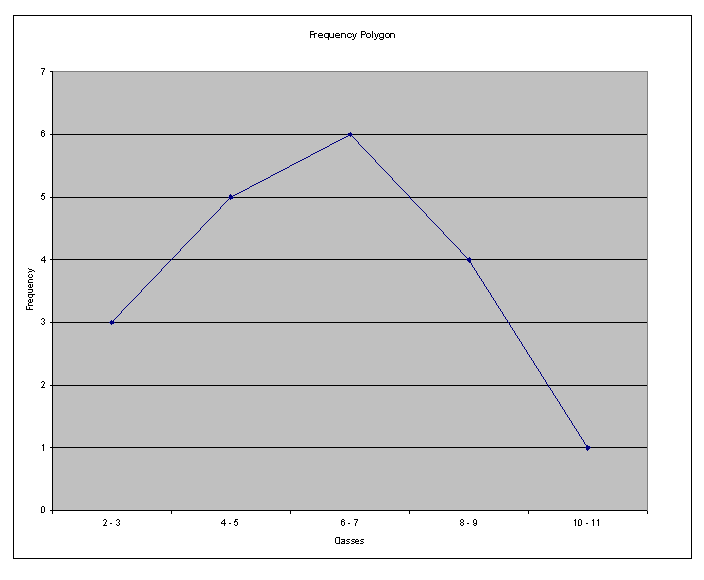
(c) (1) Die Verteilung ist ungefähr symmetrisch.
(2) Da die Verteilung ungefähr symmetrisch ist, wäre der Mittelwert das beste Maß für die zentrale Tendenz.
(3) Die Punktzahlen sind relativ über die Skala verteilt, obwohl sie sich etwas auf die Mitte konzentrieren.
