Estadísticas Tutoriales

Tutorial ANOVA

En el tutorial de esta semana, cubriremos el tema de Análisis de variación . Vea a continuación una lista de ejemplos de problemas relevantes, con soluciones paso a paso.

Esperamos que los encuentre útiles. Compartimos tutoriales completos, consejos y sugerencias con los miembros de nuestra comunidad. Por favor no dude en Contáctenos si tiene alguna pregunta.

Ejemplos de problemas de ANOVA

Pregunta 1: Se utilizó un análisis de varianza para evaluar las diferencias medias de un análisis de medidas repetidas. estudio de investigación. Los resultados se informaron como F (3,24) = 6,40.

a. ¿Cuántas condiciones de tratamiento se compararon en el estudio?

segundo. ¿Cuántas personas participaron en el estudio?

Solución: (a) Hubo 3 + 1 = 4 condiciones de tratamiento.

(b) El número total de individuos es 3 + 24 + 1 = 28.

Pregunta 2: Los siguientes datos representan los resultados de un estudio de medidas independientes que compara tres tratamientos.

a. Calcule SS para el conjunto de 3 medias de tratamiento. (Utilice las tres medias como un conjunto de n = 3 puntuaciones y calcule SS).

segundo. Usando el resultado de la parte a, calcule n (SSmedias). Tenga en cuenta que este valor es igual a SS entre (consulte la ecuación 13.6).

C. Ahora, calcule SSbetween con la fórmula computacional usando los valores de T (Ecuación 13.7). Debería obtener el mismo resultado que en la parte b.

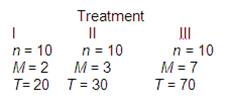
Solución: (a) Obtenemos que \(\bar{M}=\frac{2+3+7}{3}=4\)

Lo que significa que

\[S{{S}_{Means}}={{\left( 2-4 \right)}^{2}}+{{\left( 3-4 \right)}^{2}}+{{\left( 7-4 \right)}^{2}}=4+1+9=14\]

(b) Esto implica que \(n*S{{S}_{Means}}=10\times 14=140\).

\[S{{S}_{Between}}=\frac{{{20}^{2}}}{10}+\frac{{{30}^{2}}}{10}+\frac{{{70}^{2}}}{10}-\frac{{{120}^{2}}}{30}=140\]

Pregunta 3: Los daños a las viviendas causados por tuberías reventadas pueden ser costosos de reparar. Para cuando se descubre la fuga, es posible que cientos de galones de agua ya hayan inundado la casa. Las válvulas de cierre automático pueden prevenir daños extensos por agua debido a fallas en las tuberías. Las válvulas contienen sensores que cortan el flujo de agua en caso de una fuga, evitando así inundaciones. Una característica importante es el tiempo (en milisegundos) necesario para que el sensor detecte la fuga de agua. Los datos de muestra obtenidos para cuatro válvulas de cierre diferentes se encuentran en el archivo Waterflow.

a. Genere la tabla ANOVA relevante y realice una prueba de hipótesis para determinar si el tiempo medio de detección difiere entre los cuatro modelos de válvulas de cierre. Use un nivel de significancia de 0.05.
segundo. ¿Cuál es la fuente de variación entre muestras?

Válvula 1	Válvula 2	Válvula 3	Válvula 4
17	18	28	17
10	17	25	17
18	11	30	17
18	dieciséis	26	19
17	dieciséis	25	18
14	18	27	21
18	14	23	21
13	17	23	12
10	20	26	15
11	14	22	18

Solución: La siguiente tabla se obtiene a partir de los datos proporcionados

Obs.	Válvula 1	Válvula 2	Válvula 3	Válvula 4
	17	18	28	17
	10	17	25	17
	18	11	30	17
	18	dieciséis	26	19
	17	dieciséis	25	18
	14	18	27	21
	18	14	23	21
	13	17	23	12
	10	20	26	15
	11	14	22	18

Media	14,6	16,1	25,5	17,5
St. Dev.	3.406	2.558	2.461	2.677

Nos gustaría probar

\[H_0: \,\mu_{1}= \mu_{2}= \mu_{3}= \mu_{4}\]

\[H_A: \operatorname{Not all the means are equal}\]

Con los datos que se encuentran en la tabla anterior, podemos calcular los siguientes valores, que son necesarios para construir la tabla ANOVA. Tenemos:

\[SS_{Between}=\sum\limits_{i=1}^{k}{n}_{i} {\left( {\bar{x}}_{i}-\bar{\bar{x}} \right)}^{2}\]

and therefore

\[SS_{Between}={10}\left({14.6}-{18.425}\right)^2+ {10}\left({16.1}-{18.425}\right)^2+ {10}\left({25.5}-{18.425}\right)^2+ {10}\left({17.5}-{18.425}\right)^2=709.475\]

Also,

\[SS_{Within} = \sum\limits_{i=1}^{k}{\left( {n}_{i}-1 \right) s_{i}^{2}}\]

de donde obtenemos

\[SS_{Within}=\left({10}-1\right) \times {3.406}^2+ \left({10}-1\right) \times {2.558}^2+ \left({10}-1\right) \times {2.461}^2+ \left({10}-1\right) \times {2.677}^2=282.3\]

Therefore

\[MS_{Between}=\frac{SS_{Between}}{k-1}= \frac{{709.475}}{3}= {236.492}\]

De la misma manera, se obtiene que

\[MS_{Within} = \frac{SS_{Within}}{N-k}= \frac{{282.3}}{36}= {7.842}\]

Por lo tanto, las estadísticas F se calculan como

\[F=\frac{MS_{Between}}{MS_{Within}} = \frac{{236.492}}{{7.842}}= {30.1583}\]

El valor crítico para \(\alpha ={0.05}\), \(df_{1} = 3\) y \(df_{2}= {36}\) viene dado por

\[F_C = {2.8663}\]

y el valor p correspondiente es

\[p=\Pr \left( {{F}_{3,36}}> {30.1583} \right) = {0.000}\]

Se observa que el valor p es menor que el nivel de significancia \[\alpha =0.05\], por lo que rechazamos \({{H}_{0}}\). En consecuencia, tenemos suficiente evidencia para rechazar la hipótesis nula de medias iguales, al nivel de significancia de 0.05.

Resumiendo, tenemos la siguiente tabla ANOVA: