A equação do círculo
Um círculo é uma das figuras geométricas mais notáveis. Tem uma simetria notável, baseada no fato de que TODOS os pontos do círculo são equidistantes do centro, o que em inglês significa que todos os pontos do círculo estão à mesma distância do centro. Esta distância comum \(r\) é chamada de raio do círculo .
O círculo tem muitas aplicações geométricas importantes, o que o torna um objeto muito importante tanto na geometria quanto na álgebra.
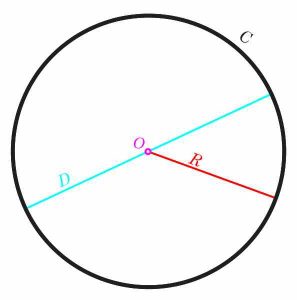
Outra propriedade crucial do círculo é que ele é facilmente representado algebricamente. Isso significa que podemos facilmente definir uma equação para representar todos os pontos em um determinado círculo. Para colocar mais concretamente, considere o plano de coordenadas \(X - Y\). Tudo isso significa que temos os eixos X e Y, que são perpendiculares entre si
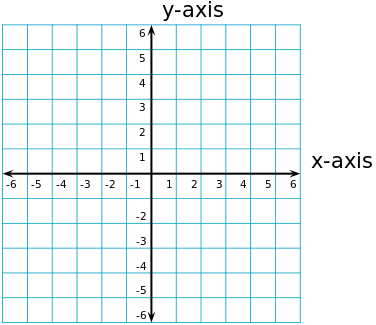
Equação do círculo
Agora, vamos falar sobre a equação que representa todos os pontos de um determinado círculo. De fato, para um círculo de raio \(r\), a seguinte equação descreve os pontos \((x, y)\) que estão no círculo:
\[\Large x^2 + y^2 = r^2\]O acima corresponde à equação de um círculo de raio \(r\), com centro localizado em \((0,0)\), origem dos eixos coordenados.
Quando o raio é \(r = 1\), temos o que é chamado de círculo unitário .
Ao olhar para a equação acima, a interpretação geométrica é que \(x\) e \(y\) são os lados de um triângulo e \(r\) é sua hipotenusa
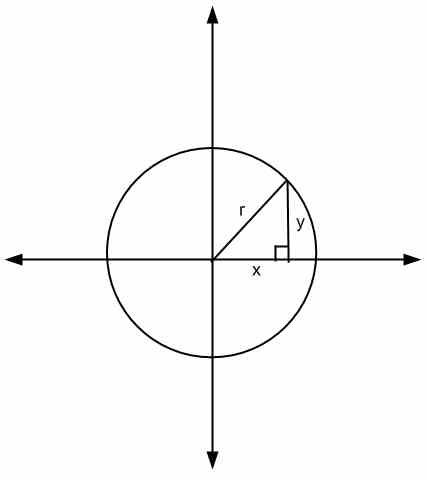
Outra maneira de ver a equação do círculo é tirar a raiz quadrada de ambos os lados da equação, então obteríamos \(\sqrt{x^2+y^2} = r\), que indica que para qualquer ponto \((x,y)\) no círculo, o distância da origem (neste caso, o centro do círculo) é igual a \(r\).
Equação de um círculo que não está centrado na origem
Uma vantagem de trabalhar em eixos coordenados é que os pontos do círculo e o centro podem ser localizado nos eixos, e pode ser representado por uma equação, como mostrado acima. Mas, em geral, o centro do círculo não precisa ser a origem, pode ser qualquer ponto \((x_0, y_0\) nos eixos coordenados, caso em que a equação do círculo se torna:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]que é conhecido como o Equação geral de um círculo . Por exemplo, digamos que você precise calcular a equação de um círculo de raio \(r = 4\), que está centrado no ponto \((1,2)\). Então, neste caso, temos \(x_0 = 1\), \(y_0 = 2\) e \(r = 4\), e então apenas colocamos esses números na equação acima e obtemos
\[\large (x-1)^2 + (y-2)^2 = 4^2\]ou também podemos escrever
\[\large (x-1)^2 + (y-2)^2 = 16\]Exemplo 1
Escreva a equação do círculo de raio 3, com centro na origem. Usando a equação, determine se o ponto (1, 2) pertence ou não ao círculo.
Resposta:
Primeiro, vamos determinar a equação do círculo. Neste caso, o círculo está centrado na origem, então \((x_0, y_0) = (0, 0)\). Portanto, a equação é
\[\large x^2 + y^2 = 3^2\]que é o mesmo que
\[\large x^2 + y^2 = 9\]Agora, a questão é se o ponto (1, 2) está ou não no círculo. Sabemos que os pontos no círculo serão tais que \(x^2 + y^2 = 9\).
Para o ponto \((1, 2)\) obtemos que \(x = 1\) e \(y=2\), então para este caso desse ponto, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) que é diferente de 9, e portanto \((1,2)\) não pertence ao círculo.
Mais sobre a equação do círculo
O círculo é uma entidade matemática tão importante, que volumes de livros foram escritos sobre ele. Os círculos cruzam a geometria, a trigonometria e a álgebra, por isso é uma aparência transversal em toda a matemática.
Como trabalhar a equação de um círculo?
Quando trabalhamos com um círculo, há várias coisas para resolver. A primeira coisa é construir a equação do círculo. Por exemplo, considere um círculo de raio \(r = 3\), que está centrado no ponto \((1,1)\).
Com base na equação geral de um círculo, a equação é
\[\large (x-1)^2 + (y-1)^2 = 3^2\]A equação acima pode ser usada, por exemplo, para determinar se um ponto pertence ao círculo ou não. O que mais você pode fazer para resolver a equação do círculo? Você poderia expandir os quadrados, então temos
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]que pode ser simplificado em
\[\large x^2 - 2x + y^2 -2y = 7\]Assim, ambas as equações são equivalentes, no sentido de que determinam o mesmo círculo. Qual você prefere? \((x-1)^2 + (y-1)^2 = 3^2\) ou \(x^2 - 2x + y^2 -2y = 7\)? É questão de gosto e para que você usaria a fórmula.
Área de um círculo
Curiosamente, para calcular o Área de um círculo , você não precisa da equação completa, você só precisa saber o raio. Em outras palavras, o área e circunferência de um círculo não dependem de seu centro.
A equação de um círculo é uma função?
Essa é uma dúvida que muitos alunos têm, e precisamos esclarecer. Em primeiro lugar, o equação do círculo é uma equação, não uma relação ou uma função.
Agora, a equação do círculo determina uma relação, e não uma função , quando você algebricamente resolva y em função de x . De fato, se resolvermos para \(y\) obtemos:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]Isso significa que para um dado \(x\), existem dois valores de \(y\) que estão associados, que são \(\sqrt{ 9 - x^2}\) e \(-\sqrt{ 9 - x^2}\), o que indica que a equação do círculo determina um relação em vez de uma função.
Um caso específico do círculo é o círculo unitário , com a equação \(x^2 + y^2 = 1\), que está centrada na origem. O círculo unitário é especialmente adequado para trabalhar com expressões trigonométricas de uma forma muito visual.
