Calculadora de probabilidade de poisson

Mais sobre a Probabilidade de distribuição de Poisson para que você possa usar melhor a calculadora de Poisson acima: O probabilidade de Poisson é um tipo de distribuição de probabilidade discreta que pode assumir valores aleatórios no intervalo $[0, +\infty)$. As principais propriedades da distribuição de Poisson são:

• É discreto e pode assumir valores de 0 a $+\infty$.


• O tipo de assimetria depende da média da população ($\lambda$)


• É determinado pela média populacional ($\lambda$)


• Sua média é $\lambda$ e sua variância populacional também é $\lambda$

Como usar a calculadora de distribuição de poisson

Usando o acima exposto Calculadora da curva de distribuição de Poisson , você pode calcular probabilidades na forma $\Pr(a \le X \le b)$, na forma $\Pr(X \le b)$ ou na forma $\Pr(X \ge a)$.

Digite o parâmetro apropriado para $\lambda$ na caixa de texto acima, selecione o tipo de coroa, especifique seu evento e calcule sua probabilidade de Poisson. Observe que $\lambda$ corresponde à média populacional da distribuição.

Como você calcula a probabilidade de poisson?

A fórmula da distribuição de probabilidade de Poisson é

$$\Pr(X = k) = \displaystyle \frac{e^{-\lambda} \lambda^k}{k!}$$

Não existe uma expressão simples ou curta para expressar o fórmula de Poisson cdf , que é obtido adicionando os valores de probabilidade individuais até um determinado valor limite.

Como você encontra a probabilidade de poisson entre dois números?

Essencialmente, você precisa avaliar a fórmula de poisson cumulativa (cdf) nos pontos finais, que seriam os dois números, digamos k e m. Mas como a distribuição é discreta, o que você calcula é F(m) - F(k-1), onde F é a função cdf de Poisson.

Agora, se você usar nossa calculadora, não precisa se preocupar com isso, basta fornecer os dois números no formulário acima.

Como calcular a distribuição de poisson calculadora excel

O Excel tem uma fórmula, a fórmula "=POISSON()" que permite obter o pdf ou o cdf de Poisson.

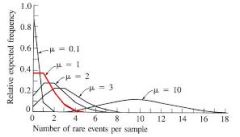
Existe alguma diferença entre a distribuição de poisson e a distribuição binomial?

Sim, há diferenças claras. Em primeiro lugar, eles não são a mesma distribuição. Embora sejam discretos (assumem valores que podem ser numerados, como 0, 1, 3, 4, etc.), eles têm algumas diferenças fundamentais.

Por exemplo, o Distribuição de veneno é determinado por apenas um parâmetro, que é sua média $\lambda$. Por outro lado, o Distribuição binomial requer um tamanho de amostra N e a probabilidade de sucesso.

Uma similaridade interessante é que ambas as distribuições de probabilidade de Poisson e Binomial podem ser aproximadas com o distribuição normal sob certas circunstâncias (tamanho da amostra suficientemente grande).

De fato, você pode verificar isso com nosso aproximação normal para o binômio e aproximação normal para a distribuição de Poisson .

Vantagens desta calculadora de poisson

1. Embora o Excel possa ajudá-lo com a maior parte do seu cálculo de estatísticas, esta calculadora mostra todas as etapas
2. Ao ver as etapas, você pode entender melhor o processo de cálculo de probabilidades
3. Em última análise, toda distribuição discreta segue a mesma lógica para calcular probabilidades

Exemplo: usos desta calculadora de probabilidade de distribuição de poisson

Pergunta : Suponha que uma variável X tenha uma distribuição de Poisson com média 3,4. Encontre a seguinte probabilidade: $\Pr(3 \le X \le 6)$.

Solução:

Precisamos de calcular uma probabilidade de distribuição binomial. São fornecidas as seguintes informações:

Population Mean $(\lambda)$ =	$3.4$
Probability Event =	$\Pr(3 \le X \le 6)$

Precisamos calcular $\Pr(3 \le X \le 6)$. Portanto, obtém-se o seguinte:

$$\Pr(3 \le X \le 6) = \sum_{i=3}^{ 6} {\Pr(X = i)} = \Pr(X = 3) + \Pr(X = 4) + \Pr(X = 5) + \Pr(X = 6)$$ $$= 0.2186 + 0.1858 + 0.1264 + 0.0716$$$$= 0.6024$$

que completa o cálculo.

Outra calculadora de distribuição de probabilidade discreta

Esta calculadora de distribuição de Poisson com etapas corresponde a um solucionador para uma distribuição discreta. Temos outras calculadoras de distribuição discreta que podem lhe interessar, como nossa Calculadora de distribuição binomial , calculadora de distribuição geométrica , e Calculadora de distribuição hipergeométrica , para citar alguns deles.

Além disso, você pode usar nosso calculadora geral de probabilidade discreta que fornecerá a média e o desvio padrão de uma distribuição discreta genérica.