Calculadora de probabilidade binomial

Mais sobre a probabilidade de distribuição binomial então você pode usar melhor esta calculadora binomial: A probabilidade binomial é um tipo de distribuição de probabilidade discreta que pode assumir valores aleatórios no intervalo de $[0, n]$, onde $n$ é o tamanho da amostra.

Propriedades da probabilidade binomial

As principais propriedades da distribuição binomial são:

• É discreto, e pode tomar valores de 0 a n, onde n é o tamanho da amostra


• O tipo de obliquidade depende dos parâmetros n e p


• É determinado por dois parâmetros: a proporção populacional de sucesso p, o tamanho da amostra n (ou número de ensaios)


• O média da distribuição binomial é $n\cdot p$ e seu desvio padrão é $\sqrt{np(1-p)}$

O que é a fórmula da probabilidade binomial?

A fórmula que define a probabilidade binomial (que é chamada a sua função de distribuição de probabilidade ) é:

\[\Pr(X = k) = \left( \begin{matrix} n \\\\ k \end{matrix} p^k \cdot (1-p)^{n-k} \]

onde n e p são os parâmetros correspondentes da distribuição. Ou seja, n é o número de tentativas e p é a probabilidade de sucesso de cada tentativa.

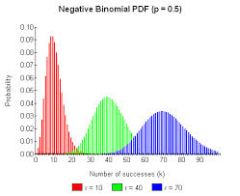
Como utilizar esta calculadora de distribuição binomial com passos

Usando o acima exposto calculadora de curva de distribuição binomial , podemos calcular probabilidades da forma $Pr(a \le X \le b)$, da forma $\Pr(X \le b)$ ou da forma $\Pr(X \ge a)$. Qualquer outro tipo de evento pode ser derivado desses tipos elementares de eventos.

Por exemplo, você pode querer encontrar a probabilidade de X estar entre 0 e 1 ou entre 3 e 4. Essa probabilidade, você calcularia como $\Pr(0 \le X \le 1) + \Pr(3 \le X \le 4)$

Digite os parâmetros apropriados para $n$ e $p$ na caixa de texto acima, selecione o tipo de cauda, especifique seu evento e calcule sua probabilidade binomial, mostrando todos os detalhes passo a passo da fórmula de probabilidade binomial.

Outras calculadoras de distribuição de probabilidade importantes

A distribuição binomial é uma espécie de distribuição discreta. Outras calculadoras disponíveis para distribuições discretas são as nossas Calculadora de distribuição de Poisson , calculadora hiper-geométrica ou o nosso calculadora de distribuição geométrica .

O que acontece quando a probabilidade de sucesso não é constante?

Uma forma generalizada do coeficiente binomial é o coeficiente multinomial , que considera combinações de números $k$ que somam $n$, com $k \ge 2$.

Agora, se estiver a lidar com distribuição contínua, pode querer verificar os nossos calculadora de probabilidade normal online que trata da distribuição normal e eventos relacionados, que é a distribuição contínua mais comum.

Exemplo: cálculo das probabilidades binomiais

Pergunta : Assuma que X é uma variável aleatória com distribuição binomial, com parâmetros n = 10 ep = 0,45. Calcule $\Pr(2\le X\le 4)$.

Solução:

Precisamos de calcular uma probabilidade de distribuição binomial. São fornecidas as seguintes informações:

Population Probability of Success $(p)$ =	$0.45$
Sample Size $(n)$ =	$10$
Probability Event =	$\Pr(2 \leq X \leq 4)$

Isto implica que

$$\Pr(2 \le X \le 4) = \Pr(X = 2) + \Pr(X = 3) + \Pr(X = 4)$$$$= \left( \begin{matrix} 10 \\\\ 2 \end{matrix}\right) 0.45^{ 2} \cdot 0.55^{ 10-2} + \left( \begin{matrix} 10 \\\\ 3 \end{matrix}\right) 0.45^{ 3} \cdot 0.55^{ 10-3} + \left( \begin{matrix} 10 \\\\ 4 \end{matrix}\right) 0.45^{ 4} \cdot 0.55^{ 10-4}$$$$= 0.0763 + 0.1665 + 0.2384$$ $$= 0.4811$$

o que significa que a probabilidade que estamos procurando é $\Pr(2 \leq X \leq 4) = 0.4811$.