Mais sobre estatísticas descritivas: usando esta calculadora de média

A Estatística Descritiva corresponde a medidas e gráficos derivados de dados de amostra e destinam-se a fornecer informações sobre a população em estudo. Dois tipos básicos de estatísticas descritivas são os medidas de tendência central e a Medidas de dispersão .

Como calcular a média?

Para calcular a média amostral, você precisa usar a seguinte fórmula:

\[ \bar X = \displaystyle \frac{1}{n} \sum_{i=1}^n X_i \]

Em termos simples, você divide a soma de todos os valores na amostra pelo número total de valores na amostra.

Como usar esta calculadora média

Para calcular a média de uma amostra, você precisa seguir estas etapas:

• Passo 1 : Identifique claramente a amostra que deseja analisar e calcule a média e certifique-se de que todos os valores sejam numéricos, caso contrário, você não poderá continuar
• Passo 2 : Se você estiver apenas calculando a média, não precisará classificar os dados. Mas se você também quiser calcular mediana e percentis , você precisará classificar os dados em ordem crescente
• Estágio 3 : Calcule o número de valores na amostra n, também conhecido como tamanho da amostra, e calcule o soma da amostra
• Passo 4 : A média da amostra é calculada dividindo a soma dos dados pelo tamanho da amostra

Portanto, para encontrar a média, você só precisa calcular a média dos dados.

A média é uma das medidas de tendência central mais comumente usadas, e por boas razões. Sabemos que, para um tamanho de amostra suficientemente grande, a média da amostra será numericamente próxima da média da população.

Em termos técnicos (eu perdi você aí, eu sei), a média da amostra é uma estimativa pontual imparcial da média da população.

Esse Calculadora média mostrará todas as etapas do processo e tudo o que você precisa fazer é digitar ou colar do Excel os dados de amostra com os quais deseja trabalhar.

Além disso, você também obtém as etapas para calcular o desvio padrão, fornecendo uma boa imagem das estatísticas descritivas mais importantes de que você precisa para começar.

Medidas de tendência central

As medidas de tendência central pretendem dar uma ideia da localização da distribuição. Exemplos de medidas de tendência central são o média da amostra \(\bar X\), o mediana e o modo.

Observe que a média da amostra é igual à média dos dados. Porém, no contexto das estatísticas, o nome mais comumente usado é média amostral.

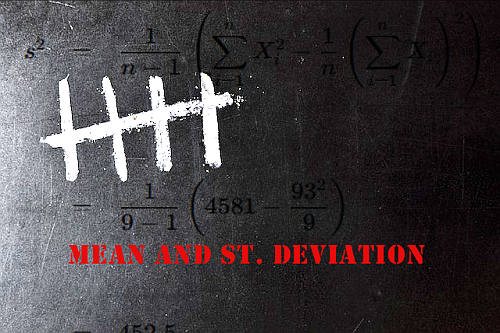
Medidas de dispersão

Exemplos de medidas de dispersão são a variância \(s^2\), o desvio padrão \(s\) e o intervalo entre outros. Diferentes medidas são mais apropriadas do que outras para determinados casos.

Por exemplo, certas medidas como a média são muito sensíveis a discrepantes , e, portanto, quando uma amostra tem outliers fortes ou é muito assimétrica, a medida preferencial de tendência central seria a mediana em vez da média da amostra

Se você deseja realizar uma análise mais completa e minuciosa, use nosso calculadora estatística descritiva .

Propriedades da média e desvio padrão

Uma excelente propriedade da média amostral é que ela é um estimador imparcial da média populacional e tem a propriedade de que, se escolhermos um tamanho amostral relativamente grande, sabemos que o valor numérico da média amostral obtida está próximo da média populacional real.

O desvio padrão da amostra, por outro lado, não é uma estimativa imparcial do desvio padrão da população, mas ainda assim, o valor numérico do desvio padrão da amostra estará próximo do verdadeiro desvio padrão da população para um grande tamanho de amostra.

Outros tipos de meios

A média da amostra, que é baseada na média dos dados da amostra, não é o único tipo de "média" que você pode conceber, pois também pode calcular a média harmônica e a média geométrica , que também tentam encontrar um elemento representativo de uma amostra, mas usando uma abordagem numérica diferente.

Encontrar um valor representativo de uma amostra realmente depende da forma da distribuição. Para distribuições distorcidas será melhor calculando para mediana ou o caminho , pois as distribuições assimétricas tenderão a super-representar a cauda assimétrica ao calcular a média.