Risolutore di equazioni quadratiche

Questo calcolatore te lo permetterà calcolare un'equazione quadratica che fornisci, mostrando tutti i passaggi. Tutto quello che devi fare è fornire un'equazione quadratica valida.

Potrebbe essere qualcosa che è già semplificato e pronto per essere risolto come x^2 + 3x + 5 = 0, puoi fornire qualcosa che non è facilmente semplificato come 3x^2 - 4x + 5/3 = x^2 +1/3x - 1, ad esempio.

Una volta fornita un'equazione quadratica valida, tutto ciò che devi fare è cliccare su "Calcola", e ti verranno fornite tutte le fasi del processo per calcolare il radici dell'equazione quadratica che viene fornito.

Di solito, utilizzerai la formula quadratica per calcolare equazioni quadratiche, ma non è l'unico modo, come vedremo nelle sezioni seguenti.

Come calcolare un'equazione quadratica?

Esistono diverse strategie per risolvere le equazioni di secondo grado. Quello più comunemente usato è l'uso del formula quadratica . Inoltre, puoi risolvere per completare i quadrati , oppure puoi risolvere per fattorizzazione quadratica .

Quali sono i passaggi per calcolare le equazioni quadratiche utilizzando la formula quadratica?

• Passaggio 1: identificare l'equazione quadratica che si desidera calcolare
• Passo 2: Assicurati che l'equazione sia completamente semplificata, altrimenti procedi con la semplificazione, fino ad avere un'equazione della forma ax² + bx + c = 0
• Passaggio 3: dopo che l'equazione è stata ridotta alla sua forma semplificata, è possibile utilizzare la formula quadratica: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Forse, usare la formula dell'equazione quadratica è il modo più pratico per trovare le radici di un'equazione quadratica, ma ci sono altri motivi per cui dovresti usare altri metodi.

Come risolvere un'equazione quadratica completando i quadrati?

Il secondo modo più comune per risolvere un'equazione quadratica è utilizzare la tecnica di completare i quadrati . Non esiste davvero una formula per completare i quadrati (sebbene tecnicamente ce ne sia una, basata sulle soluzioni dell'equazione quadratica), ma piuttosto un processo.

Quali sono i passaggi per completare i quadrati

• Passaggio 1: identifica l'equazione quadratica che desideri risolvere
• Passaggio 2: devi assicurarti che l'equazione sia completamente semplificata e che tu abbia un'equazione della forma ax² + bx + c = 0
• Passo 3: Aggiungi e sottrai un termine adatto (in questo caso, (b/(2a))² per forzare i termini del quadrato di un binomio

L'idea di forzare la comparsa di un termine della forma (x + "qualcosa)², che è l'obiettivo finale del completamento dei quadrati.

Perché dovresti usare equazioni quadratiche?

Le equazioni quadratiche appaiono costantemente nelle applicazioni di algebra sono problemi di parole. Risolvere equazioni quadratiche è un'abilità fondamentale di base che devi acquisire.

Quindi, in campi come Calculus, quando calcoli problemi di massimizzazione e minimizzazione, dovrai avere una buona familiarità con tutti i tipi di equazioni quadratiche.

Esempio: risoluzione di un'equazione quadratica

Risolvere la seguente equazione quadratica utilizzando la formula \(4x^2 + \frac{4}{3}x + 2 = 0\)

Soluzione: Dobbiamo risolvere la seguente equazione quadratica data \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

Per un'equazione quadratica della forma \(a x^2 + bx + c = 0\), le radici vengono calcolate utilizzando la seguente formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo caso, abbiamo che l'equazione che dobbiamo risolvere è \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), il che implica che i coefficienti corrispondenti sono:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

Innanzitutto, calcoleremo il discriminante per valutare la natura delle radici. La discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle -\frac{272}{9} < 0\), che è negativo, sappiamo che l'equazione data ha due diverse radici complesse coniugate.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

allora, troviamo che:

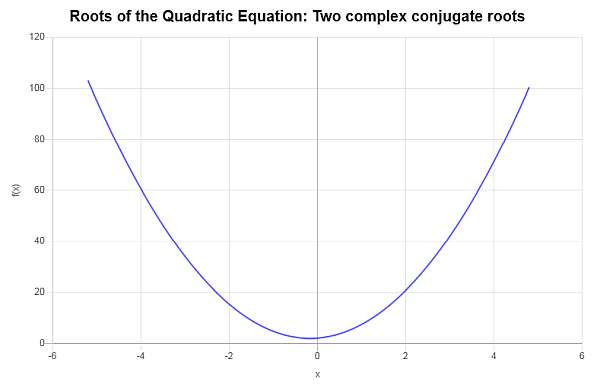
\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Pertanto, l'equazione data \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) ha due diverse radici complesse coniugate, che sono \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) e \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Graficamente:

Esempio: radice di un'equazione quadratica

Trova le radici della seguente equazione quadratica completando i quadrati \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Soluzione: In questo caso, abbiamo che l'equazione che dobbiamo risolvere è \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), il che implica che i coefficienti corrispondenti sono:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

La discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle 0 = 0\), che è zero, sappiamo che l'equazione ha una sola radice reale.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

allora, troviamo che:

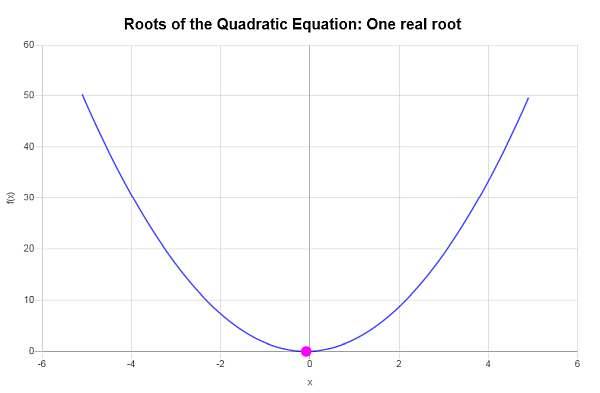
\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Pertanto, l'equazione data \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) ha una sola radice reale, che è \(x = \displaystyle -\frac{1}{12}\).

Graficamente:

Esempio: calcolo delle radici dell'equazione

Risolvere quanto segue: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Soluzione: Per questo esempio l'equazione che dobbiamo risolvere è \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), quindi i coefficienti corrispondenti sono:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

In questo caso, la discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Poiché il discriminante è \(\Delta = \displaystyle \frac{148}{9} > 0\), che è positivo, sappiamo che l'equazione avrà due radici reali diverse.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

allora, troviamo che:

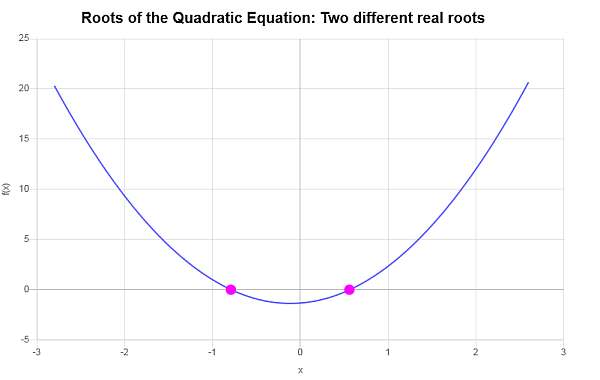
\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Pertanto, l'equazione data \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) ha due diverse radici reali, che sono \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) e \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Graficamente:

Altri utili calcolatori quadratici

Come abbiamo visto in questo tutorial, completare i quadrati gioca un ruolo fondamentale nel calcolo delle equazioni di secondo grado. Inoltre, puoi usare questo calcolatore discriminante valutare la natura delle radici (due radici reali, una radice reale o due radici complesse) senza risolvere l'equazione.

Puoi anche usare questo Calcolatore di vertici per trovare le coordinate del vertice di un'equazione quadratica, e trovare l'asse di simmetria di una parabola . Inoltre puoi esplorare questo fattorizzazione quadratica strumento per esplorare ancora un altro modo di calcolare le equazioni di secondo grado.