Le graphe d'une fonction est un ensemble de paires ordonnées \((x,y)\). Ou, le graphe d'une fonction est une conceptualisation nous faisons un ensemble de paires \((x,y)\) sur un système de coordonnées. Je dis que c'est une conceptualisation, car la façon dont nous représentons un graphe est dans une certaine mesure une illusion d'optique.

Pourquoi est-ce que je dis ça? Eh bien, jetez un œil. À quoi pensez-vous quand je dis "graphique". Vérifiez la figure avant.

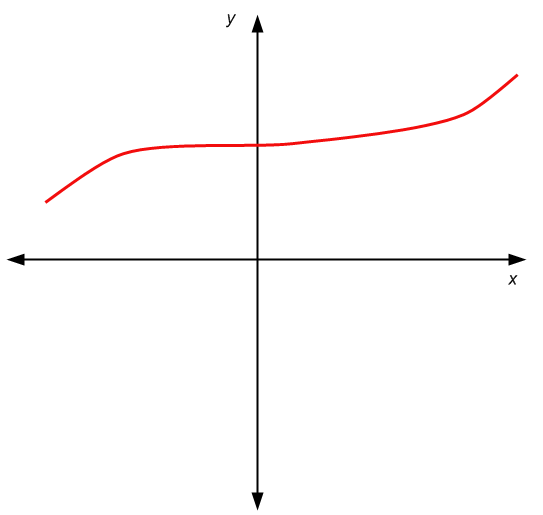
Voilà donc un graphique. Un ensemble de paires \((x, y)\), ou comme nous pouvons aussi les appeler, des points. Un point spécifique est mis en évidence ci-dessous, jetez un œil

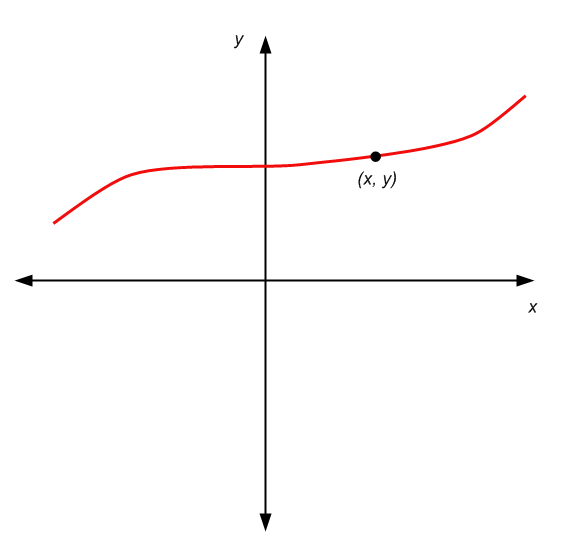
L'astuce, ou l'illusion visuelle, est qu'un point n'a, en théorie, aucune dimension (pas de largeur, pas de longueur). Donc, cette "courbe" que nous dessinons pour représenter un graphe, c'est une sorte de moyen pratique de représenter un graphe, mais nous trichons en quelque sorte, car cette représentation a une courbe qui a une épaisseur.

Donc, ce n'est pas pour pleuvoir sur votre défilé, c'est juste pour faire comprendre que ce que vous comprenez comme un graphique, c'est plutôt un représentation d'un graphique pratique et crédible.

Graphiques associés aux fonctions

Un moyen très simple de définir un graphe consiste à utiliser une fonction \(f(x)\). En effet, un graphe défini par une fonction \(f(x)\) est l'ensemble de tous les points \((x, f(x))\), pour \(x \in D\), où \(D\) est le domaine de la fonction \(f\).

La représentation est la même que les graphiques précédents, mais maintenant nous faisons ce qui suit:

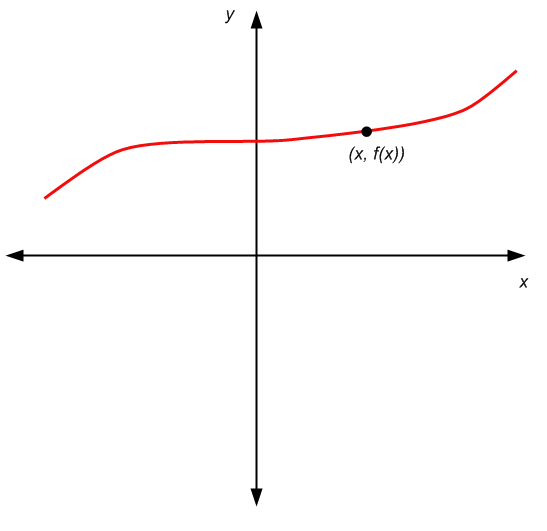
Dans ce cas, la différence la plus claire est que le deuxième composant de la paire \((x,y)\) n'est pas n'importe quelle valeur \(y\). Le deuxième composant est \(f(x)\), il est donc uniquement déterminé par \(x\).

EXEMPLE 1

Tracez le graphique de la fonction \(f(x) = x^2\).

RÉPONDRE:

Rien d'étrange, il suffit de dessiner le graphe d'une fonction. Les points du graphique sont de la forme \((x, f(x)) = (x, x^2)\). Autrement dit, la valeur de \(x\) est associée à \(x^2\) sur le graphique.

Exemples de points qui sont sur le graphique: \((1, 1)\), \((2, 2^2) = (2, 4)\), \((3, 3^2) = (3, 9)\), etc. Graphiquement, nous obtenons la représentation suivante du graphique:

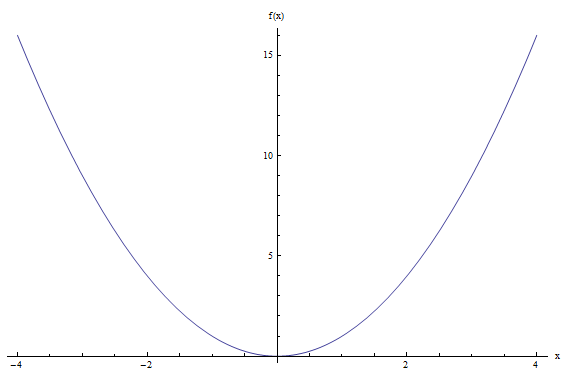
Les graphiques continuent ou interrompent

Une des hypothèses que nous faisons dans notre esprit lorsque nous pensons à un graphique est qu'il est lisse, sans sauts. Ce n'est pas toujours le cas. Il existe des fonctions qui mènent à des fonctions qui sautent, voire conduisent à des graphiques étranges. D'autres fonctions ont des graphiques très lisses, comme cela s'est produit avec \(f(x) = x^2\).

Le concept de régularité d'une fonction est formellement traité en Calcul, avec la notion de fonction continue. Mais sans trop de fuzz, on peut dire que, pour l'instant, on va penser qu'une fonction continue est une fonction qui a un graphe "lisse", et une fonction discontinue est une fonction qui n'est pas lisse, ou elle un "sauts".

EXEMPLE 2

La fonction \(f(x) = sin(x)\) est-elle continuer?

RÉPONDRE:

Eh bien, encore une fois, nous aurions besoin d'une analyse de continuité formelle pour vérifier. Mais à la lumière de la définition informelle donnée ci-dessus, vérifions son graphique. L'ordinateur nous donne ce qui suit:

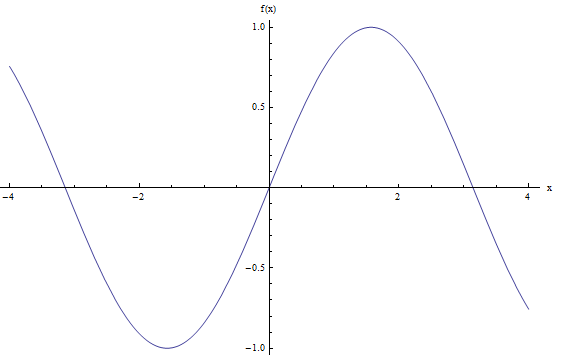
Je dirais que le graphique ci-dessus semble très lisse, sans aucun saut, donc en utilisant notre définition naïve, je dirais que \(f(x) = \sin x\) est continu.

EXEMPLE 3

La fonction \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) est-elle continuer?

RÉPONDRE:

Afin de répondre à la question, nous devons tracer le graphique. L'ordinateur nous donne ce qui suit:

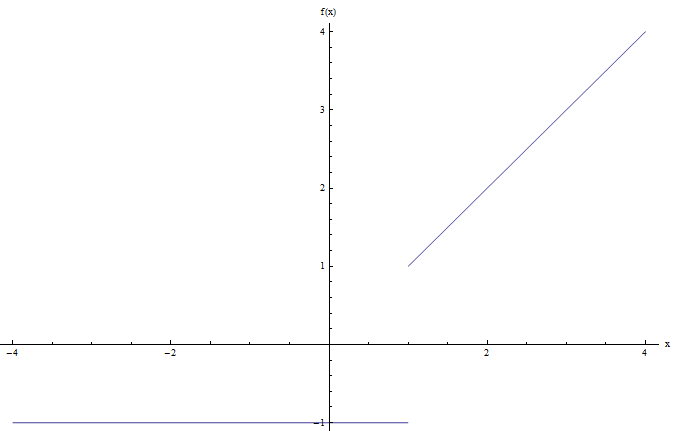
Notez qu'il y a un saut au point \(x = 1\), donc je dirais que le graphique ci-dessus a un saut, et par conséquent, cette fonction est discontinue.

En savoir plus sur les graphiques

Utiliser des graphes pour une fonction peut jouer un rôle crucial pour comprendre le comportement d'une fonction.

Il existe suffisamment d'outils analytiques (calcul) pour comprendre le comportement d'une fonction \(f(x)\), sans avoir besoin de la traceur. Mais, il est très pratique de voir un graphique car c'est un moyen très rapide de se faire une idée de ce que fait la fonction.

Que tous les graphiques ne doivent pas être notés comme provenir de fonctions. Par exemple, les graphiques peuvent également provenir de relations. Voir le graphique ci-dessous et dites-moi si vous pouvez découvrir quelle relation y est associée.

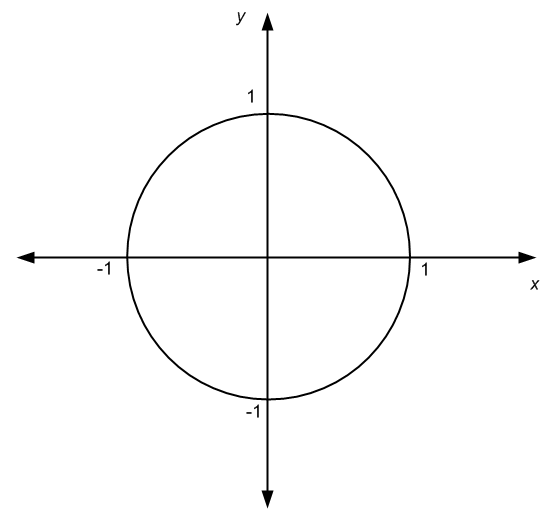
Vous avez raison, ce graphique ci-dessus est la représentation de l'équation d'un cercle unitaire, \(x^2 + y^2 = 1\), qui, comme nous le savons déjà, détermine une relation, et non une fonction.

Si vous avez besoin de construire un graphique, essayez grapher de fonction pour avoir une bonne représentation du comportement de la fonction.