En savoir plus sur ce calculateur déterminant.

En algèbre linéaire et dans l'utilisation des matrices, l'idée du déterminant d'une matrice \(A\) est un concept de la plus haute importance.

En effet, son utilisation est liée à presque toutes les opérations importantes que vous voudrez effectuer avec les matrices, telles que la vérification de l'inversibilité des matrices, trouver l'inverse d'une matrice ou systèmes de résolution .

Ainsi, où que vous regardiez autour de vous lorsque vous travaillez avec des matrices, vous trouverez des déterminants dans un sens ou dans l'autre. Il est donc très important de se familiariser avec eux.

Comment cette calculatrice matricielle peut-elle vous aider

1. Tout ce que vous avez à faire est de taper votre matrice
2. Il doit s'agir d'une matrice carrée, c'est-à-dire une matrice avec le même nombre de lignes et de colonnes
3. Cliquez simplement sur le bouton et la calculatrice vous montrera toutes les étapes et la valeur finale du déterminant
4. Travailler sur des calculs déterminants peut être extrêmement laborieux et source d'erreurs. Cette calculatrice vous évite ces problèmes

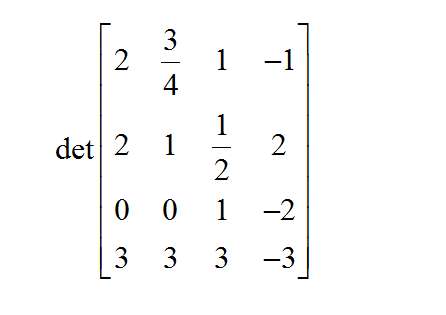
Comment calculer le déterminant d'une matrice ?

Cela pourrait être une longue réponse, car il existe de nombreuses façons de calculer le déterminant d'une matrice. Disons d'abord que les déterminants ne calculent que pour les matrices carrées (il s'agit de matrices qui ont le même nombre de lignes et de colonnes).

Ainsi, la plus petite matrice pour laquelle nous pouvons calculer un déterminant est une matrice 2x2. Considérons une matrice 2x2 générique, comme illustré ci-dessous :

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

Quelle est la formule du déterminant ? Dans ce cas, le déterminant de la matrice \(A\) est simplement calculé comme \(\det(A) = a d - bc\)

Ainsi par exemple, si nous avions :

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

le déterminant de la matrice \(A\) serait \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\). Facile, non ?

Comment trouver le déterminant d'une matrice 3x3 ?

Maintenant, pour les matrices plus grandes, nous construisons le calcul du déterminant basé sur le sous-déterminant des matrices plus petites. Juste pour vous donner une idée, voyons une façon de calculer le déterminant d'une matrice 3x3. Envisager

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

Dans ce cas, le déterminant de la matrice 3x3 matrice \(A\) est calculé sur la base de l'opération de plusieurs déterminants 2x2

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

Dans les équations ci-dessus les valeurs \(a\), \(b\), \(c\) jouent le rôle de pivots, et peuvent avoir un signe négatif. Le signe d'un pivot est \((-1)^{i+j}\), où le pivot correspondant est en ligne \(i\) et en colonne \(j\).

Par exemple \(a\) est dans la ligne 1, colonne 1, donc son signe est \((-1)^{1+1} = (-1)^2 = 1\) (positif). De plus, \(b\) est dans la ligne 1, colonne 2, donc son signe est \((-1)^{1+2} = (-1)^3 = -1\) (négatif), et ainsi de suite.

La magie consiste à choisir n'importe quelle ligne ou colonne comme pivot. Chaque pivot aura un signe associé (positif ou négatif) et un sous-déterminant, qui sont liés au cofacteurs matriciels .

Ce sous-déterminant est le véritable déterminant de la matrice d'origine après suppression de la ligne \(i\) et de la colonne \(j\), pour le pivot qui se trouve dans la ligne \(i\) et la colonne \(j\).

La convention la plus logique indique de choisir la ligne ou la colonne avec le plus de zéros pour les pivots, afin d'éviter de calculer certains des sous-déterminants, si possible.

Comment trouver le déterminant d'une matrice 3x4 ?

Tu ne peux pas le faire. Une matrice 3x4 n'est pas une matrice carrée et, par conséquent, aucun déterminant ne peut être calculé. Pour calculer un déterminant, la matrice doit avoir le même nombre de lignes et de colonnes.

Un calculateur de déterminant 4x4

Pour les matrices plus grandes, la méthodologie est la même : choisissez une ligne ou une colonne pour les pivots, idéalement celle qui contient le plus de zéros. Ensuite, trouvez le signe correspondant à chaque pivot et trouvez les sous-déterminants correspondants.

Alors, vous réduisez le calcul du déterminant d'une matrice 4x4 à l'opération de quatre déterminants 3x3. Et à leur tour, chacun des déterminants 3x3 se trouve comme l'opération de plusieurs déterminants 2x2, pour lesquels nous connaissons une formule.

Donc, ça peut vite devenir salissant.

Exemple de calcul d'un déterminant matriciel

Question: Considérez la matrice suivante :

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Calculez le déterminant de la matrice donnée, en montrant les étapes.

Solution: Nous devons calculer le déterminant de la matrice \(3 \times 3\) qui a été fournie.

En utilisant la formule du sous-déterminant, nous obtenons :

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Conclusion : Sur la base des calculs présentés ci-dessus, on trouve que le déterminant de la matrice est \(\det A = \displaystyle -15\).

Autres calculatrices matricielles utiles que vous pouvez utiliser

Les calculs matriciels effectués à la main demandent beaucoup de travail, vous pouvez donc tirer parti de nos solveurs d'algèbre linéaire.

Tout d'abord, vous pouvez utiliser cette calculatrice de matrice inverse pour calculer l'inverse d'une matrice montrant les étapes, et vous pouvez le faire soit en méthode adjointe , ou en utilisant Réduction RREF .