En savoir plus sur ce système d'équations à la calculatrice de forme matricielle

Une capacité cruciale quand Résolution de systèmes d'équations linéaires est de pouvoir passer du format traditionnel des systèmes linéaires aux matrices.

Une fois que vous avez la représentation matricielle d'un système linéaire, vous pouvez soit appliquer La règle de Cramer ou vous pouvez résoudre le système en premier trouver l'inverse de la matrice de coefficients correspondante.

Ou, avec la représentation matricielle, vous pouvez construire la matrice augmentée et appliquer la méthode de pivotement de Gauss, selon ce qui vous convient le mieux.

Premièrement : comment écrivez-vous un système d'équations sous forme matricielle ?

Étape 1: Identifier chacune des équations du système. Chaque équation correspondra à une ligne dans la représentation matricielle.

Étape 2: Allez travailler sur chaque équation. Pour chacun d'eux, identifiez le côté gauche et le côté droit de l'équation.

Étape 3: Ce qui est à gauche fera partie de la matrice A, et ce qui est à droite fera partie du vecteur b

Étape 4: Les coefficients de gauche doivent être identifiés séparément en fonction du coefficient qui multiplie chaque variable.

Étape 5 : Chaque équation représente une ligne et chaque variable représente une colonne de la matrice A.

Comment utiliser une matrice pour résoudre un système d'équations ?

Une fois que vous avez un système sous forme matricielle, vous pouvez procéder de différentes manières pour résoudre le système. Habituellement, vous commencez d'abord par calcul du déterminant de la matrice , comme critère initial pour connaître les solutions du système.

Lorsque \(\det A \ne 0\), nous savons que le système a une solution unique. Maintenant, quand \(\det A = 0\), cela ne signifie pas que vous n'avez pas de solutions, cela signifie seulement que s'il y a des solutions, ce n'est pas unique.

En effet, lorsque \(\det A = 0\), vous ne pouvez pas utiliser La méthode de Cramer ou la méthode inverse pour résoudre le système d'équations . Dans ce cas, il vaut mieux utiliser la méthode de pivotement de Gauss.

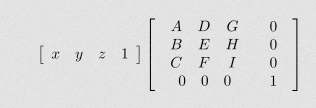
Comment résoudre des équations matricielles

Souvent, on vous donne un système d'équations directement au format matriciel. Si tel est le cas et que le nombre d'équations est le même que le nombre de variables, vous pouvez essayer d'utiliser la méthode inverse ou la règle de Cramer. Sinon, vous pouvez utiliser la méthode de Gauss.

Maintenant, vous pouvez utiliser cette calculatrice pour exprimer un système sous une forme traditionnelle lorsqu'on lui donne une forme matricielle.