Apprendre à factoriser est l'une des compétences les plus cruciales que vous puissiez acquérir. L'affacturage a tellement d'applications que vous serez heureux de prendre le temps d'en savoir plus.

Un rafraîchissement rapide sur la propriété commutative, associative et distributive. Pour les nombres réels $x$, $y$ et $z$, nous avons les propriétés suivantes

(Associativité de l'addition) $(x+y)+z = x+(y+z)$

Commutativité de l'addition) $x + y = y + x$

(Propriété distributive) $x \cdot (y+z) = x \cdot y + x \cdot z$

où $+$ et $\cdot$ sont respectivement la somme et le produit des nombres réels.

Pourquoi est-il utile de savoir factoriser?

Il existe de nombreuses raisons, mais l'une des principales est que la factorisation nous donne un moyen facile de résoudre des équations. En fait, l'affacturage est LA façon dont nous devons résoudre des équations.

Par exemple, considérons l'équation où nous essayons de résoudre pour $x$:

Comment allons-nous procéder? Eh bien, nous pouvons utiliser la propriété distributive pour obtenir:

Par conséquent, avec cette dernière expression $x(y+z) = 0$, nous avons un exemple d'affacturage. En effet, nous avons pris l'expression initiale, $xy+xz$ et l'avons factorisée dans $x(y+z)$.

Donc, maintenant, nous devons résoudre une équation plus simple, qui est $x(y+z) = 0$. Pourquoi est-ce plus simple? C'est parce que maintenant que nous savons que le produit $x(y+z)$ est égal à zéro, alors l'un des facteurs DOIT être égal à zéro.

Donc, si nous savons que $y+z = \not 0$, alors nous savons que nous devons avoir ce $x = 0$.

LEÇON : L'un des avantages de la factorisation est de pouvoir écrire une équation sous la forme d'une multiplication de facteurs égale à zéro. Alors, AU MOINS UN DES FACTEURS DOIT ÊTRE ZÉRO.

Par exemple, lorsque nous devons résoudre pour $x$ dans l'équation suivante:

nous ne réalisons pas que nous factorisons réellement quand nous le faisons

nous avons donc réduit notre équation à un produit de facteurs égal à zéro: $8x = 0$. Étant donné que l'un des facteurs $8$ n'est pas égal à zéro, la seule solution possible est $x = 0$.

En d'autres termes : si vous savez comment factoriser, vous saurez probablement comment résoudre des équations .

Comment factoriser les polynômes

L'équilibre est atteint avec une classe d'expressions très générale que l'on peut, souvent, factoriser de manière très systématique. Cette classe est la classe des polynômes. Par exemple, l'expression

est un polynôme de degré 2. Ou l'expression ci-dessous

est un polynôme de degré 3.

En général, une expression de la forme

est un polynôme de degré $n$. Naturellement, plus l'expression est simple, plus il sera facile de la simplifier, nous devrions donc essayer d'apprendre à factoriser les expressions quadratiques en premier. C'est, des polynômes de degré deux.

EXEMPLE 1

Factorisez l'expression quadratique suivante

RÉPONDRE:

Cet exemple vous montrera, exprès, qu'il peut être difficile de factoriser même l'expression la plus simple, comme celle ci-dessus. Que feriez-vous pour en tenir compte?

Et si je vous dis que vous devez ajouter zéro? C'est plutôt ridicule, non? Voyons voir:

Êtes-vous d'accord avec ce qui précède? Je viens d'ajouter $0$. Rien n'a changé. Mais que faire si je vous dis que $0 = 2x - 2x$? Donc alors

Tous les mêmes! Cela fonctionne, car j'ai ajouté zéro, donc rien ne change. Mais maintenant, nous l'étendons et le regroupons:

Alors, enfin, $x^2 + x - 2 = (x+2)(x-1)$. Rusé? Peut-être, mais c'est une façon de le faire. Bien que ce soit une manière intelligente de le faire, nous préférerions une manière plus systématique.

Factoriser un polynôme quadratique

Les astuces intelligentes sont bien, et tout ça, mais généralement nous préférerons une approche systématique, qui n'échoue jamais. Pour les polynômes quadratiques (polynômes de degré 2), il existe une manière systématique de procéder à la factorisation:

Étape 1 : Compte tenu de l'expression quadratique $ax^2 + bx + c$, nous résolvons d'abord l'équation

Étape 2 : Si les solutions (racines) de l'équation ci-dessus sont réelles (même s'il n'y a qu'une seule racine), nous appelons ces racines $x_1$ et $x_2$. Avec ces racines, nous obtenons les facteurs suivants:

donc les solutions $x_1$ et $x_2$ déterminent complètement les facteurs.

Naturellement, dans ce cas, comme prévu, la résolution d'une équation quadratique est étroitement liée à la factorisation de l'équation quadratique.

EXEMPLE 2

Factoriser l'équation quadratique suivante

en calculant ses racines.

RÉPONDRE:

Nous commençons par résoudre l'équation quadratique correspondante:

en utilisant le célèbre et bien connu formule quadratique :

ce qui implique que les solutions (racines) sont $x_1 = 1$ et $x_2 = 1$. Ensuite, l'expression quadratique $x^2 - 4x + 3$ peut être factorisée comme suit:

Observez que dans ce cas, le terme multipliant le terme $x^2$ est 1, donc dans ce cas $a = 1$.

Factorisation des polynômes avec un degré supérieur à 2

Donc, pour factoriser les polynômes quadratiques, je calcule simplement les racines de l'équation quadratique correspondante. Comment factoriser des polynômes de degré supérieur? En utilisant exactement la même méthode .

Étape 1: Étant donné l'expression polynomiale $a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0$, nous résolvons d'abord l'équation

Étape 2: Si les solutions (racines) de l'équation ci-dessus sont réelles (même si elles sont répétées), nous appelons ces racines $x_1$, $x_2$, ..., $x_n$. Avec ces racines, nous obtenons les facteurs suivants:

Ainsi, il semblerait qu'il soit tout aussi simple de factoriser un polynôme de degré 2 que de factoriser un polynôme de degré 10. Théoriquement, la réponse est oui.

Le seul problème est qu'il n'y a pas de formule algébrique simple et proche qui puisse résoudre les racines d'une équation polynomiale de degré 5 ou plus.

Parfois, nous pouvons résoudre des équations de plus haut degré en regardant le graphique, ou même en utilisant la calculatrice. Par exemple, consultez le graphique ci-dessous:

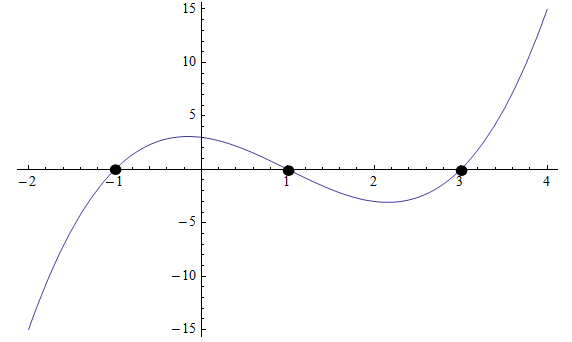
Graphiquement, nous pouvons voir que le polynôme croise l'axe des x en trois points: $x_1 = -1$, $x_2 = 1$ et $x_3 = 3$, donc ce sont les racines.

Alors, on sait que le polynôme doit être de la forme $p(x) = a(x+1)(x-1)(x-3)$. Nous aurions besoin de connaître un point de plus pour connaître la constante $a$.