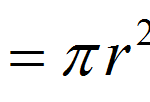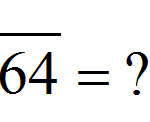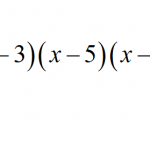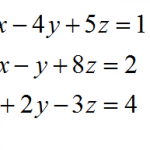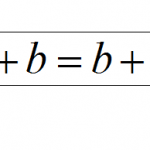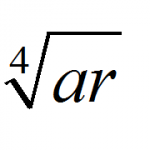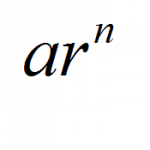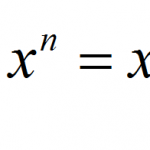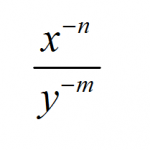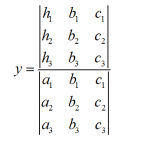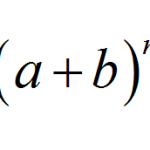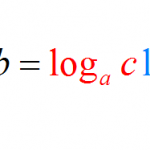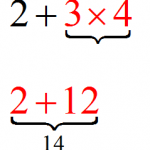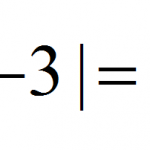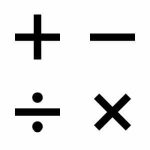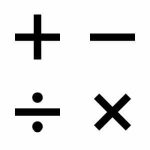Literal Equations
Literal Equations are equations where there are symbols that are not variables, but they represent a constant. So it is like an equation, but some of the numbers instead of being numbers are expressed as generic constants. In this tutorial you will ...
What is the Square Root of 64?
Sometimes a simple question like what is the square root of 64 has an answer that can confuse a few. In this case, we will dispel a couple of myths. The main objective in this tutorial is to learn a few things about square roots and radicals, so ...
Exponential Decay Formula
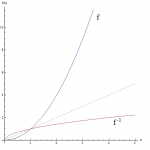
The Exponential Decay formula is a very useful one and it appears in MANY applications in practice, including the modeling of radioactive decay. Our main objective in this tutorial is to learn about the exponential decay formula, when to apply it ...
How to Find the Inverse of a Function
Many applications in Algebra and Calculus depend on knowing how to find the inverse of a function, and that is the topic of this tutorial. First of all, you need to realize that before finding the inverse of a function, you need to make sure that ...
Finding the Log Graph
The way of finding the log graph is common to all logarithmic function. This is because all logarithmic function have essentially the same shape, at least structurally, it only depends on the base of the logarithm. First, let us recall the ...
Absolute Value Inequalities
Absolute Value Inequalities are inequalities in which there is one or more absolute value. Let us recall that an inequality is almost like an equation, but instead of the \"=\" sign, we have \"≤\" or \"≥\". This difference makes it so that the ...
Factor by Grouping
Factor by grouping is an excellent way of factoring an expression, without the need of solving a polynomial equation, which could be hard to solve. The only problem of factoring by grouping is that there is not one recipe or strategy that will give ...
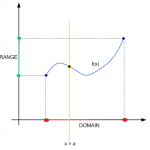
How to Find Range
Learning how to find the range of a function can prove to be very important in Algebra and Calculus, because it gives you the capability to assess what values are reached by a function. Or in other words, it allows you to find the set of all the ...
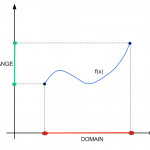
How to Find Domain
Learning how to find the domain of a function is a crucial skill in Algebra, because it gives you the capability to assess where a function is properly defined. Or in other words, the region where it is valid to operate the function The task of ...
Gaussian Elimination
Gaussian Elimination is a process conducted on matrices aimed to put a matrix into echelon form. Having a matrix in such form helps enormously to solving matrix equations very easily. Technically, the process of conducting Gaussian elimination ...
How to Factor
Learning how to factor is one of the most crucial skills you can learn. Factoring has so many applications, that you will be glad to take the time to learn all there is about it. Factoring is normally something that we take for granted, and based ...
System of Equations
A System of Equations is simply a set of two or more simultaneous equations that the need to be solved. Typically, you will be have the same number of equations and unknowns (variables), but it does not have to be the case. The only thing that is ...
Commutative Property of Addition
The Commutative Property of Addition is one of the crucial assumptions made on Mathematics, which you probably take for granted and use all the time without knowing. The idea of commutativity revolves around the order of an operation. The question ...
Simplifying Radicals
Algebraic expressions containing radicals are very common, and it is important to know how to correctly handle them. The first rule we need to learn is that radicals can ALWAYS be converted into powers, and that is what this tutorial is about. In ...
Geometric Sequences
A Geometric Sequence is a sequence of numbers that has the property that the ratio between two consecutive elements is constant, equal to a certain value (r). This value is also known as the common ratio. Assume that the first term is (a). Then, ...
Rules of Exponents
The operations with exponents are among the most common operations you will be conducting all around in Math, and it is crucial that you have a proper foundation about them. Without further ado, let us list the basic exponent properties. Using ...
Operations with Negative Exponents
The operations with exponents are among the most fundamental operations in Algebra, and among them, the ones that involve negative exponents are the ones that bring the most complications to students. First, let us recall the basic exponent ...
Cramer’s Rule
Cramer\'s Rule is a technique used to systematically solve systems of linear equations, based on the calculations of determinants. Typically, solving systems of linear equations can be messy for systems that are larger than 2x2, because there are ...
The Binomial Theorem
The Binomial Theorem is one of the more famous theorems in Algebra, and it has a multitude of applications in the fields of Algebra, Probability and Statistics. It states a nice and concise formula for the nth power of the sum of two values: ((a+b) ...
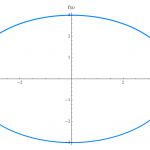
The Ellipse
An Ellipse is the geometric place of points in the coordinate axes that have the property that the sum of the distances of a given point of the ellipse to two fixed points (the foci) is equal to a constant, which we denominate (2a). The concept of ...
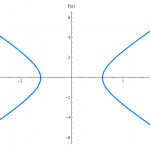
The Hyperbola
A hyperbola is the geometric place of points in the coordinate axes that have the property that the difference between the distances to two fixed points (the foci), is equal to a constant, which we denominate (2a). Naturally, that sounds a bit ...
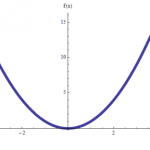
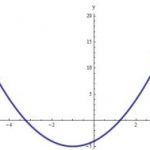
The Parabola
A parabola is the geometric place of points in the coordinate axes that have the property that they are equidistant from a fixed point (called the focus) and a line (called the directrix). I know what sounds a bit too technical, but we will go ...
Log Rules
The logarithmic function is one of the most important functions in Math, and the log rules are simple and convenient, making it really easy to work with logarithms. Let us first recall what is the meaning of (log_b a). In this context, the value ) ...
Order of Operations
The Order of Operations is a set of conventions to conduct operations for an algebraic expression (such as (2+3times 4)) when there could be an ambiguity on how to conduct the operation, because there is more than one operation. The Order of ...
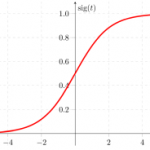
The Graph of a Function
The graph of a function is a set of ordered pairs ((x,y)). Or, the graph of a function is a conceptualization we do a set of pairs ((x,y)) on a coordinate system. I say it is a conceptualization, because the way we represent a graph is to a degree ...
The Unit Circle
The unit circle is one of the most used \"laboratories\" for understanding many Math concepts. The unit circle crosses Algebra (with equation of the circle), Geometry (with angles, triangles and Pythagorean Theorem) and Trigonometry (sine, cosine, ...
Domain and Range
The domain of a function is a set where a function is well defined. More specifically, let (f: D rightarrow R) be a function, which means that (f(a)) is well defined for (a in D). The domain of the function (f) is the set (D). Mathematically you ...
The Absolute Value
The absolute value of a number corresponds to its magnitude, without considering its sign, if it has it. Geometrically, it corresponds to the distance of a point (x) to the origin (0), on the real line Mathematically the absolute value of a number ...
Commutative Property
The Commutative property is one of those properties of algebraic operations that we do not bat an eye for, because it is usually taken for granted. The commutative property has to do with the order of the operation between two operands, and how it ...
Associative Property
The associative property is one of those properties that does not get much talk about, because it is taken for granted, and it is used all the time, without knowing. The associative property has to do with what operands we process first when ...
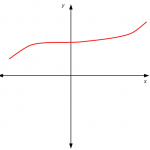
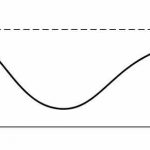
Horizontal Asymptotes
A Horizontal Asymptote is an upper bound, which you can imagine as a horizontal line that sets a limit for the behavior of the graph of a given function. This means that the graph of the function (f(x)) sort of approaches to this horizontal line, ...
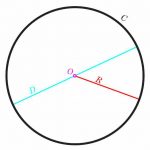
The Equation of the Circle
A circle is one of the most notable geometric figures. It has some remarkable symmetry, based on the fact that ALL points in the circle are equidistant from the center, which in English means that all the points in the circle are the same distance ...
Fractions and Their Operations
A fraction corresponds to a number of the form where (a) and (b) are integer numbers, and it can be thought as \"(a) divided by (b)\". For example, the numbers are fractions. The only restriction for the fraction ( displaystyle{frac{a}{b}}) is ...
The Quadratic Equation Formula: The meaning of the term -b/2a
You have probably wondered many times what is the meaning of the quadratic formula. I mean, you probably know how to use the formula, this is, if you are presented with a problem involving some kind of quadratic equation, you know that the ...
Functions: What They Are and How to Deal with Them
The concept of function is extremely important and it is absolutely omnipresent in Math. That is why we need to give it a good brush up, before attempting to understand some of the goodies that will come afterwards when go deeper into Calculus ...
Math Cracks – A Cool Approach to Integration by Parts
Introduction The idea of integration by parts sounds quite scary for many Calculus students, and I think there is a good reason for that. First of all, integration by parts is a technique that involves two steps (or more) instead of one step as ...
In case you have any suggestion, or if you would like to report a broken solver/calculator, please do not hesitate to contact us .