A Geometric Sequence is a sequence of numbers that has the property that the ratio between two consecutive elements is constant, equal to a certain value \(r\). This value is also known as the common ratio.

In a real life problem, you will be given an initial value \(a\), and the constant ratio \(r\) that is preserved between consecutive values in the sequence. Your task will be to compute the geometric sequence using this given information.

How do I solve a geometric sequence?

Assume that the first term is \(a\). Then, the next term is \(a r\), and the next is \(ar^2\). And so on.

So, in other words, we start with the first term \(a\), and the next term is always found by multiplying the previous term by \(r\).

So the first term is \(a_1 = a\).

The second term is \(a_2 = a r\).

The third term is \(a_3 = a r^2\).

Geometric sequence formula

By looking at the above example, what happens is that is initial value \(a\) is multiplied by an extra \(r\) at each step. Therefore, the general n ^th term is

This means that after going forward \(n\) steps, we get that the corresponding number in the sequence is \( a_n = a r^{n-1}\). This is the formula for the geometric series pattern, and all you need is to plug in the values of \(a\) and \(n\) in the formula.

So, how do you find the nth term in a geometric sequence?

Summarizing, in order to find the nth term in a geometric sequence, you need two pieces of information to define a geometric sequence: You need the initial term \(a\), and the constant ratio \(r\).

Then, the consecutive terms of the geometric sequence are obtained by multiplying the previous term by \(r\). For example, 3, 6, 12, 24, ... is a geometric sequence since the initial value is \(a = 3\) and then each subsequent value is obtained by multiplying the previous value by \(r = 2\).

Also, for example, you can ask yourself what is the rule for 1 2 4 8 16, and whether it is geometric sequence. Well, we have that the initial value is \(a = 1\), and each next value is obtained by multiplying the previous value by \(r = 2\).

EXAMPLE 1: Example of a geometric sequence

Find the 6th term of a geometric sequence with initial term \(10\), and \(r = 1/2\).

ANSWER:

So, how do you calculate a geometric sequence? Based on the information provided, we have enough information to define the geometric sequence. Indeed, we have the first term \(a = 10\), and we have the constant ratio \(r = 1/2\).

The general n ^th term is

so then the 6 ^th term is

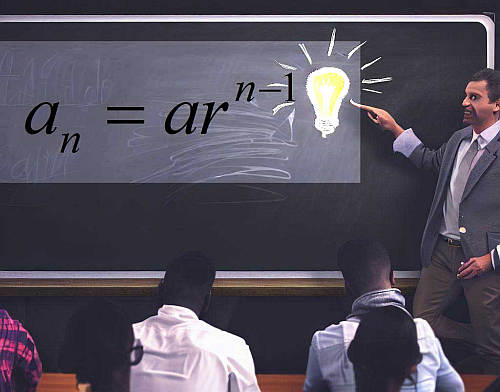
Can the Common Ratio be Negative?

Yes, absolutely. The constant ratio \(r\) can be negative. For example, we can have a geometric sequence with initial term \(a_1 = 1\) and constant ratio \(r = -2\). So then, the second term is \(a_2 = 1 \cdot (-2) = -2\), \(a_3 = (-2) \cdot (-2) = 4\), and so on.

So, it is the exactly the same rule: in order to the following term, we multiply the previous term by the constant ratio \(r\), even if the constant ratio is negative.

EXAMPLE 2

Find the 5th term of a geometric sequence with initial term \(3\), and \(r = -2\).

ANSWER:

We have enough information to define the geometric sequence, because we have the first term \(a_1 = 3\), and we have the constant ratio \(r = -2\).

The general n ^th term (with negative constant ratio) is

so then the 5 ^th term is

You can use our geometric sequence formula calculator to double check what you have found above, which is a explicit formula calculator.

EXAMPLE 3

Consider the sequence 1, 1/2, 1/4, 1/16, ... Is this sequence geometric?

ANSWER:

In order for a given sequence to be geometric, the terms need to have a common ratio. In this case, dividing the second term by the first term we get \((1/2)/1 = 1/2\).

Then, if we divide the third by the second term: \((1/4)/(1/2) = 1/2\). So far so good.

Now, if we divide the fourth by the third term: \((1/16)/(1/4) = 1/4\). It fails. It is not a geometric series, because it does not have a common ratio (the ratio is 1/2 for the first two terms, but then it is 1/4, so it is not constant).

Hence, the sequence is NOT a geometric sequence.