Literal Equations
Literal Equations are equations where there are symbols that are not variables, but they represent a constant. So it is like an equation, but some of the numbers instead of being numbers are expressed as generic constants.
In this tutorial you will learn how to handle literal equations, and how to operate with them.
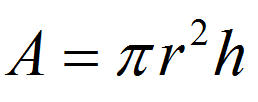
What is a Literal Equation
The first task on hand is to specify what a literal equation is. When we say "literal", we are referring to "letters". Yes, from Latin literal comes from "letters"
So, a literal equation is an equation that involves lots of "letters", as opposed to numbers. Those letters are not supposed to be variables, they are supposed to represent numbers, in terms of a generic constant.
Therefore, in order to identify a literal equation, we must see lots of letters, of which one (or potentially more) is the actual
variable
.
Like in any other equation, the idea is to solve for the variable (which means, to isolate the variable on one side of the equation).
For example, consider the formula for the volume of a cylinder of radius \(r\) and height \(h\):
\[V = \pi r^2 h\]This is a literal equation. Why? Because we have an equation with many letters.
The question is what is the variable and what are the constants. In truth, that is subjective, to a degree.
For example, one could argue that \(V\) is the variable, and \(r\) and \(h\) are the literals (or constants), and it would make sense.
But one could say that for example, we are given the volume \(V\) and height \(h\), and you need to find the radius \(r\). In that case we have the same literal equation, but the variable would be \(r\).
It is relevant to know what is the variable in a literal equation, in order to know what are we solving for.
Strategies to Deal with a Literal Equation
So, we have a literal equation, now what? Well, like every other equation, we should try to solve it.
This means, we need to isolate the variable on one side of the equation, and put everything else, using all available algebraic rules, on the other side.
This means, in practical terms, that we are expressing the variable in terms (or as a function) of the constants (literals).
The process of solving literal equations is the same as the one for solving regular equations:
We add, subtract, multiply or divide terms on both sides of the equality in order to isolate the variable.
There is not one way of doing the solving, it depends on the characteristics and the structure of the equation.
Examples of Solving Literal Equations
The fastest way to learn a skill in Math is to PRACTICE. Here we go.
EXAMPLE 1:
Let us come back to the cylinder example. For a cylinder with given volume \(V\) and height \(h\), find its radius \(r\)
ANSWER:
We know that the formula for the volume of a cylinder is
\[\large V = \pi r^2 h\]For the above literal equation, we have that the variable (the one we want to solve for) is \(r\) and the constants (given values) are \(V\) and \(h\).
The process of solving for \(r\) is shown below:
\[\large V = \pi r^2 h\] \[\large \displaystyle \Rightarrow \frac{V}{\pi h} = r^2\] \[\large \displaystyle \Rightarrow \sqrt{\frac{V}{\pi h}} = r\]Therefore, the literal equation is solved, because we have \(r\) isolated on one side of the equality, and the rest on the other side.
EXAMPLE 2:
Solve the following literal equation:
\[\large m n = \frac{x-y}{k} \]for \(x\).
ANSWER:
In this case we are explicitly told that the variable is \(x\), so then all the other letters are constants for the purposes of solving the equation.
The following is obtained when solving for \(x\):
\[\large m n = \displaystyle \frac{x-y}{k} \] \[\large m n k = x-y \] \[\large m n k+y = x \]which ends the calculation.
More About Solving Literal Equations
Why do we make a fuzz about the difference between literal equations and regular equations?? Actually, we don't make a fuzz. A literal equation is an equation, first and foremost.
The conceptual exercise is in realizing that regardless of whether we have a number or a constant that represents a generic number, the process of solving the equation is identical. That is the key concept.
How to Solve Literal Equations with Fractions
So what happens if you find fractions when you solve a literal equation with fractions? Well, the same as you would do with a regular equation: if you want to eliminate something that is in the denominator, you multiply both sides of the equation by it, and if you want to eliminate something that is in the numerator, you divide both sides of the equation by it.
Is there any strategy that works better?
Not really. Depending on the type of equation you have, you may use some specific strategies to make your job easier. For example, if you have a logarithmic equation (an equation in which the variable is inside of a logarithm), we are better of making efficient use of the log rules to solve those equations efficiently.