How to Find the Inverse of a Function
Many applications in Algebra and Calculus depend on knowing how to find the inverse of a function, and that is the topic of this tutorial.
First of all, you need to realize that before finding the inverse of a function, you need to make sure that such inverse exists.
The good thing about the method for finding the inverse that we will use is that we will find the inverse and find out whether or not it exists at the same time.
Ready?? Buckle up then.

How Can You Tell if a Function Has an Inverse?
Technically, a function has an inverse when it is one-to-one (injective) and surjective.
The crucial condition though is that it needs to be one-to-one, because a function can be made surjective by restricting its range to its own image.
![]() How do you know when a function is one-to-one?
How do you know when a function is one-to-one?
Well, there are at least a couple of ways. One is the algebraic way, and the other way is the graphical way (I bet I know which one you prefer, huh?)
![]() Algebraic Way
Algebraic Way
For the algebraic way, in order for a function \(f\) to be one-to-one, we need to prove that every time that \(f(x) = f(y)\), we need to have that \(x = y\).
In other words, we need to prove that
\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]
![]() Graphical Way
Graphical Way
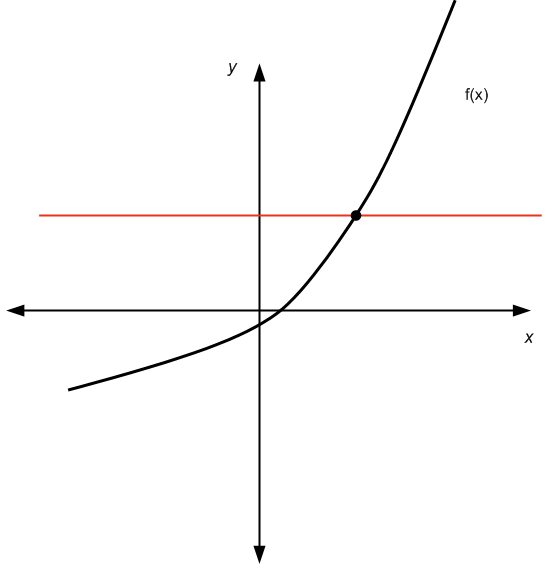
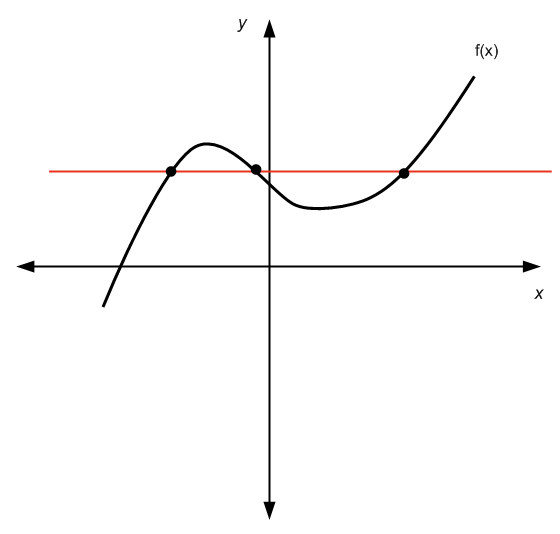
For the graphical way, we need to use the horizontal line test : For any horizontal line we draw, the graph of the function crosses at most once that horizontal line.
Graphically:
It passes the horizontal line test
It does not pass the horizontal line test
Finding the Inverse
Finding the inverse of a given function \(f(x)\) requires you to solve an equation.
Indeed, you have the equation \(f(x) = y\), you take \(y\) as a given number, and you need to solve it for \(x\), and you need to make sure that the solution is UNIQUE.
That is all. Easy, right??
Now, onto the practical steps:
![]() Step 1:
For a given \(y\), set the equation:
Step 1:
For a given \(y\), set the equation:
and solve it for \(x\).
![]() Step 2:
Make sure you pay attention to see for which \(y\), there is actually a solution that is unique.
Step 2:
Make sure you pay attention to see for which \(y\), there is actually a solution that is unique.
![]() Step 3:
Once you solve \(x\) in terms of \(y\), that expression that depends on \(y\) will be your \(f^{-1}(y)\).
Step 3:
Once you solve \(x\) in terms of \(y\), that expression that depends on \(y\) will be your \(f^{-1}(y)\).
![]() Step 4:
Change the variable name from \(y\) to \(x\) and the you have your inverse function \(f^{-1}(x)\).
Step 4:
Change the variable name from \(y\) to \(x\) and the you have your inverse function \(f^{-1}(x)\).
EXAMPLE 1
Find the inverse of the function \(f(x) = \sqrt x\)
ANSWER:
So, we take \(y\) as given and we need to solve \(f(x) = y\), which in this case it corresponds to solving
\[\sqrt x = y\]Notice that the square root is always non-negative, so in order to have a solution, we need that \(y\ge 0\).
Applying square to both sides we get that
\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]So then, \(f^{-1}(y) = y^2\), and switching the variable name, we have the inverse function is
\[f^{-1}(x) = x^2\]for \(x\ge 0\).
EXAMPLE 2
Find the inverse of the function \(f(x) = \displaystyle \frac{x}{x+1}\), for \(x > -1\)
ANSWER:
Again, we take \(y\) as given, and now we need to solve for \(x\) the equation \(f(x) = y\). So we have
\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x - yx = y\] \[\Rightarrow \,\, x(1 - y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]So then, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\), and switching the variable name, we have the inverse function is
\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]More About Finding the Inverse of a Function
One of the crucial properties of the inverse function \(f^{-1}(x)\) is that \(f(f^{-1}(x)) = x\).
Think about what this thing is saying. Something like: "The function evaluated at the inverse gives you the identity".
Or in other words, evaluating the inverse through the function is like doing nothing to the argument.
Or like some people like to say: The function can cancels the inverse in a way.
You choose your version.
How to find the inverse of a quadratic function? Can You?
Actually, the answer is: it depends. This is because if we consider a quadratic function on the whole real line , then it is not 1-to-1, since it does not pass the horizontal line test, as you can see in the chart below:
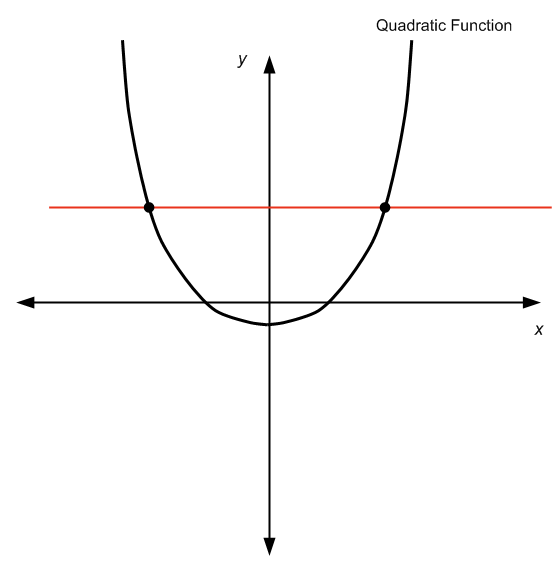
By not passing the horizontal line test, we can see that for a given \(y\) there is more than one \(x\) value so that \(f(x) = y\), so we cannot "solve" for \(x\), since there is more than one \(x\).
BUT, if you restrict the domain, and consider say only the positive numbers, we would get the following:
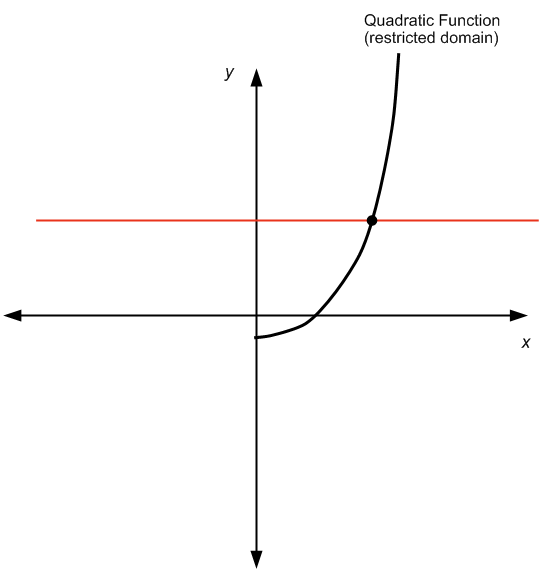
which passes the horizontal line test, and hence, the quadratic function is invertible.
MORAL OF THE STORY: In order to check if something is invertible, it is NOT only about the function. It is about the function AND its domain and range .
How to Quickly Figure out Inverse Functions Graph
There is always the requirement of assessing whether or not the function \(f(x)\) is invertible or not (by checking whether or not it is one-to-one). But assuming that you know it is invertible, there is an easy way of finding the graph of the inverse.
![]() First, graph the given function \(f(x)\).
First, graph the given function \(f(x)\).
![]() Then, graph the 45 degrees line \(y = x\).
Then, graph the 45 degrees line \(y = x\).
![]() To graph \(f^{-1}(x)\), all you have to do is to reflect the graph of \(f(x)\) through the 45 degrees line \(y = x\), like a mirrow.
To graph \(f^{-1}(x)\), all you have to do is to reflect the graph of \(f(x)\) through the 45 degrees line \(y = x\), like a mirrow.
See the example below with the functions \(f(x) = \sin x\) and \(f^{-1}(x) = \arcsin x\)
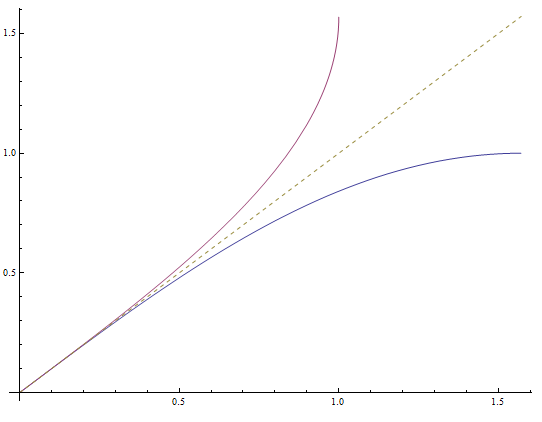
Another way to see this, is to use the original graph and change the value of \(x\) by the value of \(y\).
Is there any way for a function be its own inverse?
Yes, it is actually possible, but it only happens for the identity function, this is, with \(f(x) = x\).
