The Ellipse
An Ellipse is the geometric place of points in the coordinate axes that have the property that the sum of the distances of a given point of the ellipse to two fixed points (the foci) is equal to a constant, which we denominate \(2a\).
The concept of a "geometric place" is very appealing from a conceptual point of view, but it may not give you a clear view of what you are trying to depict.
Try and do the exercise of looking a the equation below and see if you can figure out what it looks like graphically;
Could you figure out how the graph by just looking at the equation above. I thought so. Let me introduce the ellipse for you:
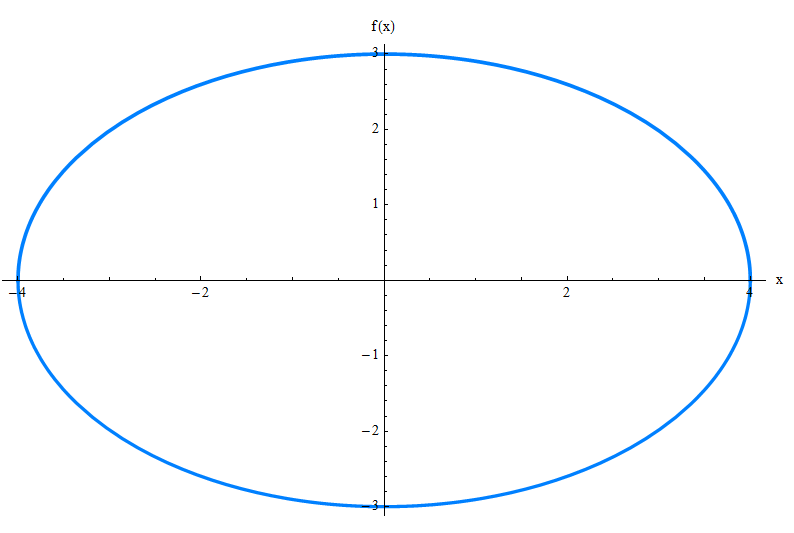
The General Equation of the Ellipse
Without much of a theoretical discussion, we will state that the general equation of the ellipse with center at the origin, and with foci on the x-axis, for \(a \ge b\) is
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
For the ellipse described above, it has foci at points \((-c, 0)\) and \((c, 0)\), where \(c = \sqrt{a^2 - b^2}\).
Now what happens with the equation of the above hyperbola when \(b > a\)?
In that case, the foci are on the y-axis, and they are \((0, -c)\) and \((0, c)\), where \(c = \sqrt{b^2 - a^2}\).
Now, if we wanted to displace the center to a point \((k,h)\)?
All you have to do in that case is replace \(x\) by \(x-k\), and replace \(y\) by \(x-h\).
Hence, by doing a translation, we get that the equation of a general ellipse is
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]The above ellipse has a center at \((k,h)\) and it has foci at \((k-c, h)\) and \((k+c, h)\) where \(c = \sqrt{a^2 - b^2}\) for \(a \ge b\), and \((k, h-c)\) and \((k, h+c)\) where \(c = \sqrt{b^2 - a^2}\) for \(b>a\).
EXAMPLE 1
Find the foci, of the ellipse:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]ANSWER:
First of all, based on the structure of the equation above, the ellipse is centered at the origin \((0, 0)\). Notice that the major semi axis is 4, which is associated with \(9y\), so then the foci is on the y-axis.
From the equation we obtained that \(a^2 = 9\) and \(b^2 = 16\). We find that \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Therefore, the foci are at \((0, -\sqrt{7})\) and \((0, \sqrt{7})\).
EXAMPLE 2
Find the equation of the ellipse centered at \((0, 2)\) with one focus at \((6, 2)\) and a semi-minor axis with a size of 3.
ANSWER:
Based on the information provided, \(c = 6 - 0 = 6\). Since the foci are on a like that is parallel to the x-axis, we get that \(b = 3\) and then \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)
Therefore, the equation of the ellipse is:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]The Ellipse and general Conic Sections
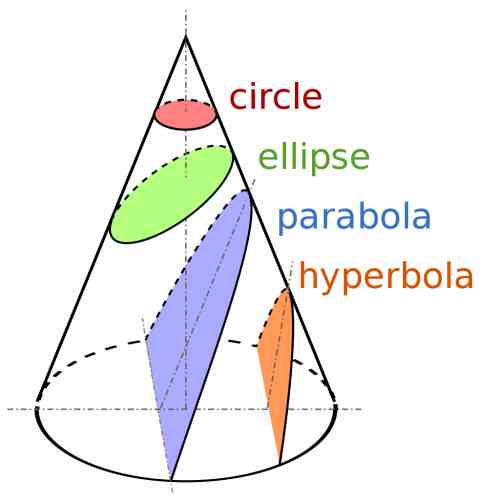
Same as with the case of the parabola, the hyperbola and the circle, the ellipse is tightly related to the cone. Ancient Greek mathematician named Apollonius discovered this connection, with what is called conic sections .
A conic section corresponds to the shapes that are formed when you make a cut through a cone with a plane, and depending on the relative angle of the cone and the plane, the shape of the cross section changes.
Indeed, depending on the angle the cone and plane face each other, the shape of the cross section can be a parabola, circle, ellipse, or an hyperbola. This is depicted in the graph below:
More About the Ellipse
For an ellipse with equation \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \), with \(a \ge b\), \(a\) is called the semi-major axis, and \(b\) is called the semi-minor axis.
Now for, \(b > a\), that denomination is reversed, so \(a\) would be called the semi-minor axis, and \(b\) is called the semi-major axis.
Eccentricity
The eccentricity of an ellipse is computed by using the following formula:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]This eccentricity parameter shows indicates how much the shape of the ellipse departs from a symmetric version of the ellipse (which is the circle, which has eccentricity \(e = 1\)).
Applications
The ellipse has so many applications. In science, it is extensively used in Astronomy. Indeed, the planets describe elliptic orbits around the sun.
Algebraically an ellipse resembles a lot to a hyperbola, but their properties are radically different.
You may also be interested in learning about the parabola, for which you can check this tutorial . You can also take a look at our hyperbola tutorial . Finally, you can also learn all there is to learn about the circle .