Absolute Value Inequalities
Absolute Value Inequalities are inequalities in which there is one or more absolute value . Let us recall that an inequality is almost like an equation, but instead of the "=" sign, we have "≤" or "≥".
This difference makes it so that the solution set is typically a region, like for most inequalities. And the fact that there absolute values involved indicate a certain especial treatment for their resolution.
In this tutorial we will concentrate on the specific skills required for the resolution of this type of inequality that contains one ore more absolute values. Also, we will assume that one or two variables, \(x\) and/or \(y\) are involved in the inequality.
What is an Absolute Value Inequality?
For the purpose of this analysis, we will consider an absolute value inequality to be an inequality involving one or two variables, with at least one absolute value.
For example, below we have an absolute value inequality with two variables \(x\) and \(y\):
\[|3x+2y-1| \ge 1\]Or also, we could have the following absolute value inequality with only one variable:
\[|3x-1| \le 2\]For our purposes, and for the purpose of the techniques used for their resolution, we will deal with both types inequalities (one and two variables)
How to Solve Absolute Value Inequalities?
When solving equations or inequalities, there is not really a silver bullet that solves everything. Each problem is different and may have its own peculiarities.
The best we can do is to provide a series of steps that will aid you in the process of solving an inequality.
![]() Step 1:
For each absolute determine the regions in which the argument of the absolute value is negative and where it is non-negative.
Step 1:
For each absolute determine the regions in which the argument of the absolute value is negative and where it is non-negative.
![]() Step 2:
If there is only one absolute value in the inequality, solve it in both areas (where the argument of the absolute value is negative, and where it is non-negative).
Step 2:
If there is only one absolute value in the inequality, solve it in both areas (where the argument of the absolute value is negative, and where it is non-negative).
![]() Step 3:
If there is more than one absolute value in the inequality, you need to intersect all the regions in order to get a set of smaller partitions. In each partition, you need to know EXACTLY the sign of each argument. Then, solve the inequality in all the areas.
Step 3:
If there is more than one absolute value in the inequality, you need to intersect all the regions in order to get a set of smaller partitions. In each partition, you need to know EXACTLY the sign of each argument. Then, solve the inequality in all the areas.
![]() Step 4:
Once you get the part solution that is in each of the areas, the final solution is the simply the union of these part solutions.
Step 4:
Once you get the part solution that is in each of the areas, the final solution is the simply the union of these part solutions.
In simple words: You need to find out the regions where you know exactly the sign of the argument of the absolute values (so you can get rid of them).
A couple of examples should clarify these steps.
EXAMPLE 1
Solve the following inequality
\[| 2x + 4y - 1 | \ge 2\]ANSWER:
In order to solve the inequality, we need to use the steps that were specified above.
Step 1: There is only one absolute value, so we need to determine whether is the argument negative and non-negative. Therefore, we need to solve first:
\[2x + 4y - 1 \ge 0\]There are several strategies to solve the above, but the easiest one is to first solve the equation
\[2x + 4y - 1 = 0\]which means that \(4y = -2x + 1\) or the same as \(y = -\frac{1}{2}x + \frac{1}{4}\), which corresponds to a line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{1}{4}\).
Now, to take care of \(2x + 4y - 1 \ge 0\) we test whether the point \((0,0)\) satisfies or not the inequality:
\[2(0) + 4(0) - 1 = -1 < 0\]So, \((0,0)\) satisfies or not the inequality. The conclusion is that the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{1}{4}\) divides the plane in two regions:
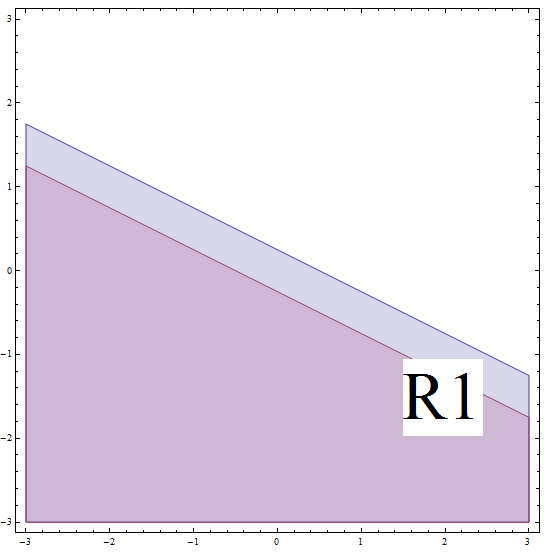
![]() For the points below the line (we call this region 1, \(R_1\)), we get that \(2x + 4y - 1 < 0\)
For the points below the line (we call this region 1, \(R_1\)), we get that \(2x + 4y - 1 < 0\)
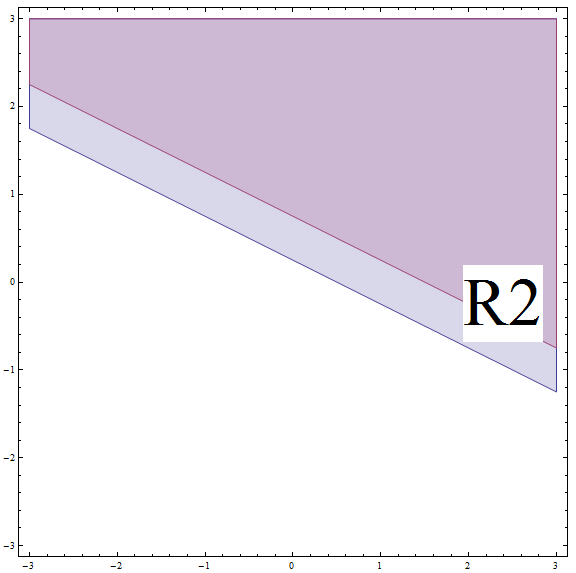
![]() For the points above the line , including the line itself (we call this region 2, \(R_2\)) we get that \(2x + 4y - 1 \ge 0\)
For the points above the line , including the line itself (we call this region 2, \(R_2\)) we get that \(2x + 4y - 1 \ge 0\)
Why is this important? Why we take all this trouble? Because on \(R_1\), we get that since \( 2x + 4y - 1 < 0\), then \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). Similarly, on \(R_2\), we get that since \( 2x + 4y - 1 \ge 0\), then \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Step 2: Now we need to solve the inequality on region 1, \(R_1\) :
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]This corresponds to all the points below or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = -\frac{1}{4}\). But don't forget that you are on \(R_1\), and this line we found is BELOW the boundary of \(R_1\) (see the graph below).
To clarify, since we are under the assumption that we are in \(R_1\), we need to have that we are BELOW line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{1}{4}\). Under this assumption, we solved the original inequality and we also need to be below line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = -\frac{1}{4}\). These two conditions must happen simultaneously, so we get the intersection of the two regions.
So then, the part solution in this case corresponds to all the points below or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = -\frac{1}{4}\).
Now we need to solve the inequality on region 2, \(R_2\) :
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]This corresponds to all the points above or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{3}{4}\). But don't forget that you are on \(R_2\), and this line is ABOVE the boundary of\(R_2\) (see the graph below).
By finding the intersection between \(R_2\) and the region above, we get that the part solution in this case is all the points above or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{3}{4}\).
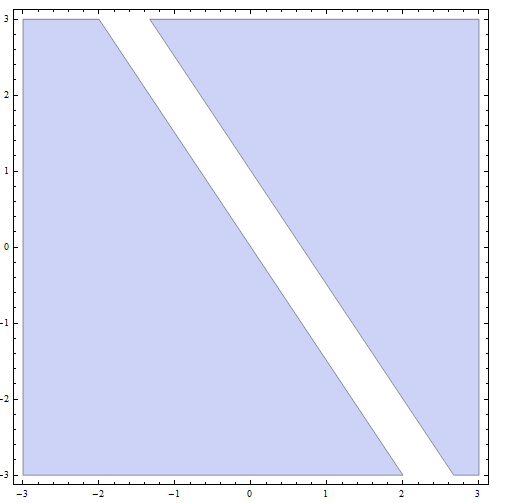
Step 4: Now, the final solution is the union of all part solutions from the previous parts: The final solution is all the points BELOW or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = -\frac{1}{4}\), PLUS all the points ABOVE or on the line with slope \(m = -\frac{1}{2}\) and y-intercept \(n = \frac{3}{4}\).
Graphically, we get
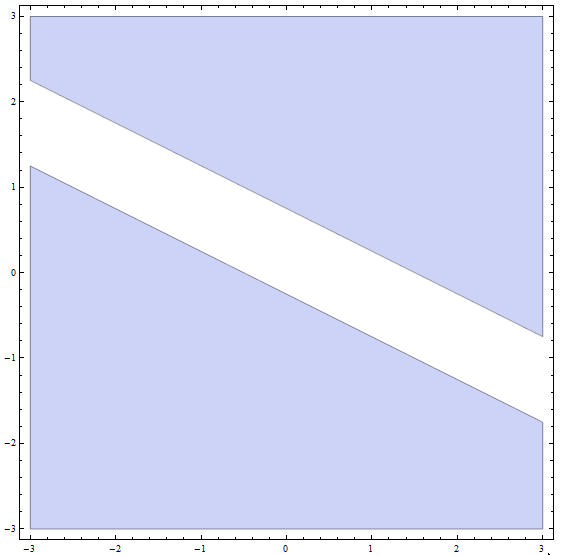
which concludes the resolution of the inequality.
EXAMPLE 2
Solve the following double absolute value inequality
\[| 2x - 1 | \ge |x + 3|\]ANSWER:
This is a double absolute value inequality because there are 2 absolute values. This means that finding the regions will take a bit more of work (relatively speaking).
Step 1: For the first absolute value we solve:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]So we get that \(2x- 1 \ge 0\) on \([\frac{1}{2}, +\infty)\), and \(2x- 1 < 0\) on \((-\infty, \frac{1}{2})\).
For the second absolute value we solve:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]So we get that \(x+3 \ge 0\) on \([-3, +\infty)\), and \(x+3 < 0\) on \((-\infty, -3)\).
So then, we define 4 regions:
![]() \(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). On this region we get: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). On this region we get: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
![]() \(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). On this region we get: \(2x- 1 \ge 0\) AND \(x+3 < 0\), though this region is empty.
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). On this region we get: \(2x- 1 \ge 0\) AND \(x+3 < 0\), though this region is empty.
![]() \(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). On this region we get: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). On this region we get: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
![]() \(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). On this region we get: \(2x- 1 < 0\) AND \(x+3 < 0\).
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). On this region we get: \(2x- 1 < 0\) AND \(x+3 < 0\).
Step 2: Now we need to solve the double absolute value inequality on each of the four regions:
• On \(R_1\):
Here we get \(2x- 1 \ge 0\) AND \(x+3 \ge 0\) so then
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]So, in order to get the part solution we need to intersect \(x \ge 4\), or \([4, +\infty)\) with \(R_1\).
The corresponding part solution is therefore: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• On \(R_2\):
This part solution is empty (\(\varnothing\)).
• On \(R_3\):
Here we get \(2x- 1 < 0\) AND \(x+3 \ge 0\) so then
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]So, in order to get this part solution we need to intersect \( x \le -\frac{2}{3}\), or \( (-\infty, -\frac{2}{3}]\) with \(R_3\).
The corresponding part solution is therefore: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• On \(R_4\):
Here we get \(2x- 1 < 0\) AND \(x+3 < 0\) so then
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]So, in order to get this part solution we need to intersect \( x \le 4 \), or \((-\infty, 4]\) with \(R_4\).
The corresponding part solution is therefore: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
![]() Step 4:
Finally, we get the union of the part solutions, to get that the solution of the initial given inequality is
Step 4:
Finally, we get the union of the part solutions, to get that the solution of the initial given inequality is
No one said it would short, right? Well. It is not really tough, you just have to be systematic and stick to the plan.
More About Inequalities with Absolute Value
Why do we even worry about this kind of inequalities? We care because they do have applications in practice.
For example, in geometry, the distances in the real line need to be represented as an absolute value, because it needs to be non-negative.
One could have a certain geometric situation in which you need to find all the points in the real line that are at least at a distance of 2 from the point 3. Such situation can be described with the following inequality:
\[| x-3 |\ge 2\]Let us understand the above inequality. The point \(x\) is the point we want to satisfy the inequality. The distance from \(x\) to the point 3 is represented by \(|x - 3|\).
Then, we are trying to find the points that are at least at a distance of 2 from the point 3, so then the distance \(|x - 3|\) needs to be at least 2, which explains the \(|x - 3| \ge 2.\)
This is just one kind of absolute value inequalities problems that you can find in practice.
Can you find absolute value inequalities with no solution
You bet. Here you have one \(|2x| < |x|\). It is possible for an inequality to be simply unfeasible like the case of this one I just gave you.
How about graphing absolute value inequalities?
The process of graphing them is essentially hand in hand with the process of solving them: You need to find the regions where you know exactly whether the arguments of the absolute values are positive or negative.
Also, whenever possible you want to simplify parentheses when the associative law applies (not always the case).
Then the absolute value inequalities become into simple inequalities, which is trivially graphed. Then, all the pieces of the regions obtained are simply joined.
