Sometimes a simple question like what is the square root of 64 has an answer that can confuse a few. In this case, we will dispel a couple of myths.

The main objective in this tutorial is to learn a few things about square roots and radicals, so that you are able to answer questions about it without hesitation.

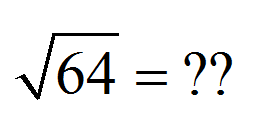
So, what is the square √ 64?

First thing is first. Before giving the answer, let us spell out the definition of the square root:

The square root of a given number is the positive number (or zero) so that when squared results in that given number .

That is it. So, given a number $x$, its square root is a number $b$ so that $b \ge 0$ and

By looking at the above expression, we can see that if $b$ is going to be the square root of $x$, then $x = b^2$, and since a square number cannot be negative, $x$ can only be non-negative (if we want to be able to find its square root).

Conclusion : We can only compute square roots of non-negative values $x$. Or said differently, the domain of the function $\sqrt x$ is $[0,+\infty)$.

So then, answering our initial question: What is the Square Root of 64?

Based on what we defined, we need to find a non-negative value $b$ so that $b^2 = 64$. Any number meeting those properties come to mind?

Well, yes, what if we tried with $b = 8$? Ok, so $b = 8$ is non-negative, and $b^2 = 8^2 = 64$.

So then, we have found the square root of 64, which is 8, because 8 is non-negative, and $8^2 = 64$. We write this as:

The Myth About the Square Root Function: What are all the possible answers of √ 64?

Now we go to the topic that motivated this tutorial... The above definition given of the square root allows us to discard the common statement that "the square root of 64 is plus or minus 8" , which is wrong. Indeed

Now, we can understand why such myth carries on. Indeed, both 8 and -8 have the property that $8^2 = 64$ and $(-8)^2 = 64$. So then, why is -8 NOT the square root of 64?

Because by definition, we said that the square root needs to be that non-negative number that has the property that when squared they equal the given number. And -8 fails the condition of being non-negative.

How to find square root?

The process of finding a square root, say $\sqrt x$, depends on what the value of $x$ is. For example, if $x$ is negative, then $\sqrt x$ will not be a real number.

What does that mean? It means, that there is no real number such that squaring it leads to a negative output. That is what we mean when we say that $\sqrt {-4}$ is not real, which means that there is no real number $b$ with the property that $b^2 = -4$.

Notice that we say there is no real number with that property, because as a matter of fact, we can get a COMPLEX number that has that property. In fact, if you square the complex number $2i$, what you get is

Fascinating, isn't it?. So, we know we cannot solve $\sqrt x$ when $x$ is negative.

Now, what happens when $x = 0$? That case is simple, as we know that $0^2 = 0$, so we know that $\sqrt 0 = 0$.

So then, now we are left with the case of when $x$ is positive. In that case, the square root will exist and it will be a real number. Now, whether or not we can find it EXACTLY, it will depend on whether or not the number is a perfect square or not.

Not all numbers are perfect squares. Indeed, the first perfect squares are 1, 4, 9, 16, 25, etc. It is a reduced list of numbers that gets more far more distant from each others. You can only find the square root EXACTLY of perfect squares. For the rest of numbers, you will need approximations.

Example: How to solve √ 625?

In this case, to solve $\sqrt 625$, we see that 625 is positive, so as we said before, the square root can be solved. But also, 625 happens to be a perfect square, since $625 = 25^2$.

Hence, in order to solve $\sqrt 625$, we notice that $625 = 25^2$, which implies that $\sqrt 625 = 25$.

Example: How to solve √ 4?

Very similar to the previous case, when we want to solve $\sqrt 4$, we observe that that 4 is positive, so we know the square root can be solved. Also, 4 is a perfect square, since $4 = 2^2$.

Hence, to solve $\sqrt 4$, we notice that $4 = 2^2$, so we conclude that $\sqrt 4 = 4$.

Example: How to solve √ 2?

Now this case is different, when we want to solve $\sqrt 3$, and we notice that 2 is positive, so we know the square root can be solved. But, 2 is NOT a perfect square.

Hence, to solve $\sqrt 2$, we know it exists, but we can not write it exactly. Indeed, we can prove that $\sqrt 2$ is an irrational number and it corresponds to an infinite sequence of decimals, that does not repeat itself.

So in this case, by "solving" $\sqrt 2$ we mean we know it exists, but we cannot write it exactly. But we can write a very good rounded approximation, if we wanted to.

The Graph of the Square Root Function

Look at the graph of the square root function below:

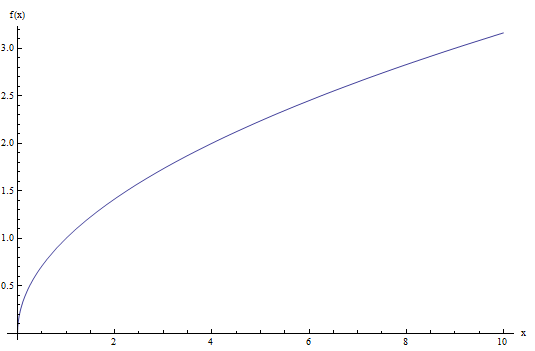
As you can see, that function only takes non-negative values, and it actually passes the vertical line test, so it is a function.

So in the end, the definition of the square root as the non-negative $b$ so that $b^2 = x$ makes the square root a function.

If indeed we had that $\sqrt{64} = \pm 8$, then $\sqrt x$ would not be a function, would be a relation instead, because the vertical line at $x = 64$ would cross the graph twice (at 8 and -8).

What About Other Radical Functions?

There are other types of radical functions. For example, the cubic root $\sqrt[3] x$. In this case, there is no need to make a rule for what radical to choose from, because the cubic root of a given number $x$ is the number $b$ so that $b^3 = x$.

Cubic Root

For the cubic root case, there is no need to make distinctions because for a given $x$ there will be just ONE number $b$ such that $b^3 = x$.

For example

simply because $4^3 = 64$. Or

simply because $(-4)^3 = -64$. This is, there is no ambiguity like in the case of the square root.

Quartic Root

For the quartic root case, it is similar to the square root. We will have that $\sqrt[4] x = b$ if $b \ge 0$ and $b^4 = x$.

For example

because $2^4 = 16$ and $2 \ge 0$. But

because although $(-2)^4 = -16$, we have that $-2 < 0$ so then the non-negativity condition is not met.

How about for the n-th root $\sqrt[n] x$ in general???.

I am sure you guessed it.

For $n$ even, the situation is like the square root: $\sqrt[n] x = b$ if $b \ge 0$ and $b^n = x$.

For $n$ odd, the situation is like the square root: $\sqrt[n] x = b$ if $b^n = x$.