How to Find Domain
Learning how to find the domain of a function is a crucial skill in Algebra, because it gives you the capability to assess where a function is properly defined. Or in other words, the region where it is valid to operate the function
The task of finding where it is valid to operate a function is a useful one. For example, consider the function \(f(x) = \sqrt x\). We know that the function operates values such that \(x \ge 0\). We cannot work with negative numbers, because we would get something like \(f(-1) = \sqrt{-1}\), which is not well defined (at least as a real number)
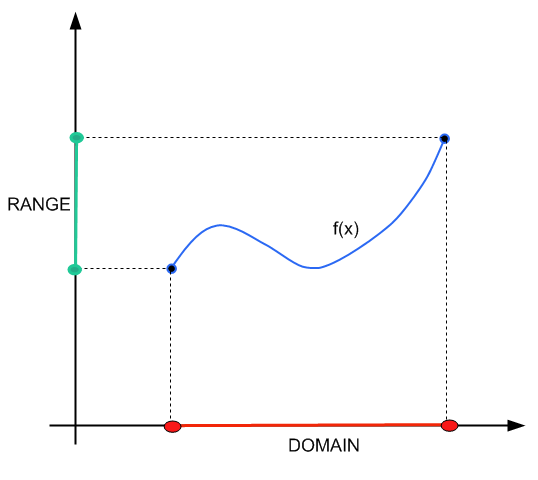
You can check our previous tutorial in which we talked in depth about the domain and range . This tutorial will be oriented towards the operational part of finding the domain.
Why Do We need to Find the Domain?
The reason why we need to find the domain of a function is that each function has a specific set of values where it is defined. Not all functions are defined everywhere in the real line.
The domain the region in the real line where it is valid to work with the function \(f(x)\), in terms of the values that \(x\) can take.
What Do We Need to Do to Find the Domain?
Really, there is not one trick that fits all sizes. Each function is different and different strategies need to be used to find the domain, depending on the function.
There are two techniques you ALWAYS need to take into account:
![]() Technique 1
: Ensure that there are divisions by zero.
Technique 1
: Ensure that there are divisions by zero.
Moreover, those points that lead to a division by zero need to be excluded from the domain.
![]() Technique 2
: Ensure that there are divisions square roots with negative arguments (like \(\sqrt{-1}\)).
Technique 2
: Ensure that there are divisions square roots with negative arguments (like \(\sqrt{-1}\)).
Moreover, those points that lead to a square root of a negative number need to be excluded from the domain.
Ultimately, using these two techniques you should be able to weed out the points that are not in the domain. The rest of points in the real line ARE part of the domain, simply.
So, these two techniques solve the problem of knowing how to find the domain of a function algebraically. Another way of doing so is by looking at the graph, if available.
EXAMPLE 1
Find the domain of the function \(f(x) = \sqrt{x+4}+3\)
ANSWER:
The first thing we need to do, and there is where our success in finding the domain lies on, is to determine where potentially we could find invalid operations, such as divisions by zero, or negative square roots.
For the function \(f(x) = \sqrt{x+4}+3\), there are no potential divisions by zero, but there is a square root. In order to have valid argument, the argument inside of the square root must be non-negative.
Therefore, in order for \(x\) to be in the domain of the function, we need to have \(x\ge 0\). This implies that the domain of \(f\) is \(\{x: x\ge 0\}\), or \([0, +\infty)\) if we use interval notation.
Is is always that easy?? Not really, it can get as hard as you get, depending on the complexity of the function \(f(x)\).
Normally, though, the examples you see in your tests and homework are rather simple. Let's us hit a notch higher in terms of difficulty.
EXAMPLE 2
Now find the domain of the function \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
ANSWER:
This function is a bit more complex and requires a more careful treatment. In this case, we need to worry of both possible divisions by zero and negative square roots.
First, there could be a potential division by zero, when \(x = 3\), which indicates that \(x = 3\) should be excluded from the domain.
Now, we need to take care of a potential negative square root. We need to assess the sign of \(\displaystyle \frac{x+4}{x-3}\). Moreover, we need it to be non-negative, so we need to solve:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]In order for a division to be non-negative, we need either both numerator and denominator to be positive, or both numerator and denominator to be negative.
In other words, we need that both \(x+4 \ge 0\) and \(x-3 > 0\), or both \(x+4 \le 0\) and \(x-3 < 0\).
This is the same that both \(x \ge -4\) and \(x > 3\), or both \(x \le -4\) and \(x < 3\).
And this can be written as \(x > 3\), or both \(x \le -4\), which corresponds to the interval \( (-\infty, -4] \cup (3, +\infty)\).
The conclusion is that the domain of the function \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) is:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]As you can see, the difficulty level increased a bit, and you can actually increase it as much as you want.
How to Find Domain of a Rational Function
First of all, let us recall that a rational function is the quotient of two polynomials, of the form:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]How do you find the domain for the above rational function? We need to follow our rule: look for potential divisions by zero and negative square roots.
In this case, there are no potential negative square roots, but there could be divisions by zero, wherever the polynomial that is in the denominator is zero.
The conclusion is very simple: The domain of a rational function is the whole real line EXCEPT for those points in which the polynomial in the denominator is zero.
EXAMPLE 3
Find the domain of
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]ANSWER:
First of all, we need to understand that this is a rational function, because you have two polynomial \(p(x) = x^2 + x + 1\) and \(q(x) = x^3 - 6x^2 + 11x - 6\) in the numerator and denominator, respectively.
So then, the first step is to find the zeros of the polynomial in the denominator, so we need to solve: \[ x^3 - 6x^2 + 11x - 6 = 0\]
That equation is sort of difficult to solve, so I will give you that indeed \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), so then we need to solve:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]which means that the roots of the polynomial in the denominator are \(x_1 = 1, x_2 = 2, x_3 = 3\). The conclusion is that the domain of the function is the whole real line, except for the points 1, 2 and 3. Using interval notation, the domain is \((-\infty, +\infty) \backslash \{1,2,3\}\).
Other Strategies for Finding Domain of a Function
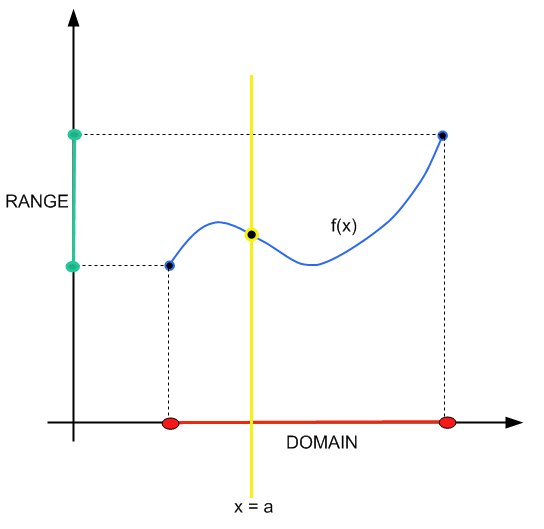
The alternative of finding the domain of a function by looking at potential divisions by zero or negative square roots, which is the analytical way, is by looking at the graph.
The method is simple: you construct a vertical line \(x = a\). If that vertical line crosses the graph of the function at one and only one point, then \(x = a\) belongs to the domain.
Short and sweet.
Finally, how do you find the domain of a function with a square root
This is the core of one of the techniques that we have been talking about, which is to find potential negative square roots. So then, when you have a function with one or more square root, you know that it is very likely that you will have a potential negative root, and you need to detect it.
This not always the case, though. Think of the function \(f(x) = \sqrt{x^2}\). That function has a a square root, but the argument inside is \(x^2\), which cannot be negative, so we have a case of a function with a square root that does not have negative square roots.
