Exponential Decay Formula
The Exponential Decay formula is a very useful one and it appears in MANY applications in practice, including the modeling of radioactive decay.
Our main objective in this tutorial is to learn about the exponential decay formula, when to apply it and how to deal with its parameters.
Algebraically speaking, an exponential decay expression is any expression of the form
\[\large f(x) = A e^{-kx}\]where \(k\) is a real number such that \(k > 0\), and also \(A\) is a real number such that \(A > 0\).
Typically, the parameter \(A\) is called the initial value , and the parameter \(k\) is called the decay constant or decay rate .
For example
\[\large f(x) = e^{-x} \]and
\[\large g(x) = e^{-2x} \]both correspond to functions with exponential decay.
How do those functions with exponential decay look GRAPHICALLY? Check it out below:
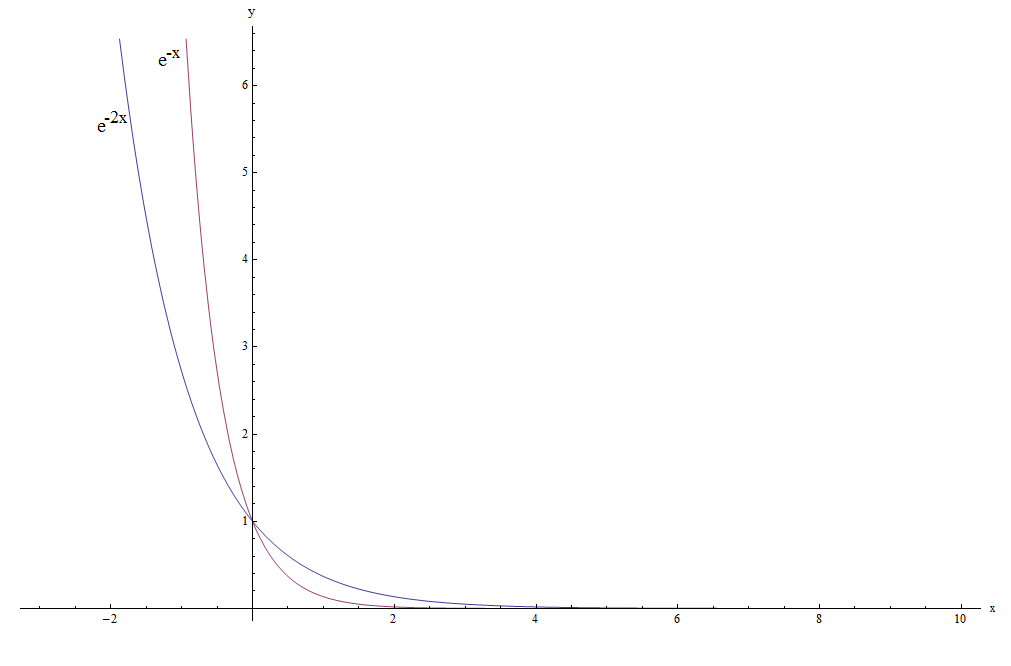
One thing we can observe is that both functions DECAY REALLY fast.
What do we mean by DECAY??? They decay, in the sense that they rapidly approach to zero as \(x\) becomes larger and larger (\(x \to +\infty\)).
Indeed, both functions after say \(x > 4\) are very small (the graph almost touches the y-axis).
Also, if we pay attention, we realize that \(e^{-2x}\) decays FASTER than \(e^{-x}\).
QUESTION :
Does the function below:
\[\large f(x) = 2^{-x}\]have exponential decay???
The answer is YES.
Although you could initially think: "Well, that is not exponential decay, because I do not see the '\(e\)' anywhere ... ". So, that is very observant.
BUT, don't forget that we can write
\[\large 2 = e^{\ln 2}\]so then the function
\[\large f(x) = 2^{-x}\]can be re-written as
\[\large f(x) = 2^{-x} = \left(e^{\ln 2}\right)^{-x} = e^{-(\ln 2) x}\]The above calculation proves (cough, cough, sorry I know you don't like that word) that \(2^{-x}\) is a function with exponential decay with decay constant \(k = \ln 2\).
EXAMPLE 1:
Find the initial value and decay rate for the following function:
\[\large f(x) = 3 e^{-4x}\]ANSWER:
Based on the given function, we get directly that the initial value in this case is \(A = 3\) and the decay rate is \(k = -4\).
EXAMPLE 2:
Determine whether the expression below has exponential decay, and if so, find its initial value and decay rate:
\[\large g(x) = \displaystyle \frac{1}{2} 3^{-2x}\]ANSWER:
Notice that we don't see the '\(e\) directly in the expression, BUT, don't forget that we can write
\[\large 3 = e^{\ln 3}\]so then the function
\[\large g(x) = \displaystyle \frac{1}{2} 3^{-2x}\]can be re-written as
\[\large g(x) = \displaystyle \frac{1}{2} 3^{-2x} = \frac{1}{2} \left(e^{\ln 3}\right)^{-2x} = \frac{1}{2} e^{-2(\ln 3) x}\]Therefore, this is a function with exponential decay, and its parameters are: Initial value \(A =\frac{1}{2}\) and exponential decay \(k = 2(\ln 3)\).
Applications: How to Find the parameters of an Exponential Formula
Often times we are not just given the exponential decay parameters. Yeah. Sometimes those parameters need to be calculated from certain information provided, and then you need to concern yourself about how to solve the exponential decay
That information is usually given in one of the following two types:
Type 1:
We know there is exponential decay, AND we are given the initial value and the
half-life
Type 2:
We know there is exponential decay, AND we are given the value of the function at two different points in time.
Notes about the Half-Life
The half-time corresponds to the time a function with exponential decay takes to takes its value to half of its original value.
So, assume that \(h\) is the half life of \(f(x) = A e^{-kx}\) and \(A\) is known. How do we calculate the decay rate \(k\)?? Observe that when \(x = h\) we will have exactly HALF of what we had initially:
\[A/2 = f(h) = A e^{-k h}\]and solving this leads to
\[A/2 = A e^{-k h}\] \[\Rightarrow \displaystyle \frac{1}{2}= e^{-k h}\] \[\Rightarrow \displaystyle \ln\left(\frac{1}{2}\right)= \ln\left(e^{-k h}\right)\] \[\Rightarrow \displaystyle -\ln 2 = -k h\] \[\Rightarrow \displaystyle k = \frac{1}{h} \ln 2\]When working on an actual problem you can either use the formula directly, or simply do the derivation we did by setting up the information about the half-life.
EXAMPLE 3:
Assume that a function has an initial value of \(A = 3\), and its half life is \(h = 3\). Also, assume that the function has exponential decay. Find the exponential decay rate.
ANSWER:
So, this is the first case of the type of information we can be given. We need to find the initial value \(A\) and the decay rate \(k\) in order to fully determine the exponential decay formula.
In this case, we are given already that \(A = 3\), so all we have left is to compute the decay constant \(k\). Since we know the half-life, we can compute the decay rate directly using the formula:
\[ \displaystyle k = \frac{1}{h} \ln 2 = \frac{1}{3} \ln 2 \approx 0.231049 \]Hence, the exponential decay formula is
\[f(x) = \displaystyle A e^{-k x} = 3 e^{-\frac{1}{3} \ln 2 x} \approx 3 e^{-0.231049 x} \]EXAMPLE 4:
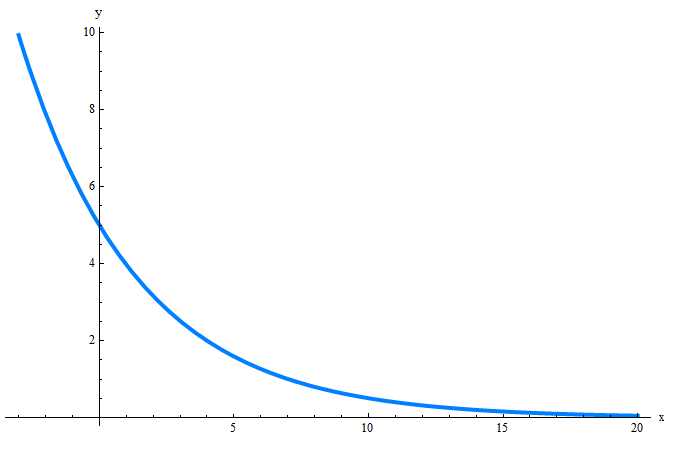
Assume that a function has an initial value of \(A = 5\), and when \(x = 4\) we have that \(f(4) = 2\). Also, assume that the function has exponential decay. Find the exponential decay formula.
ANSWER:
So, this is the first case of the type of information we can be given. We need to find the initial value \(A\) and the decay rate \(k\) in order to fully determine the exponential decay formula.
In this case, we are given that \(A = 5\), and then all we have to compute is the decay constant \(k\). Since we know the value of the function when \(x = 4\):
\[ 2 = f(4) = 5 e^{-k \cdot 4}\] \[\Rightarrow 2 = 5 e^{-4k}\] \[\displaystyle \Rightarrow \frac{2}{5} = e^{-4k}\] \[\displaystyle \Rightarrow \ln\left(\frac{2}{5}\right) = \ln\left(e^{-4k}\right)\] \[\displaystyle \Rightarrow \ln 2 - \ln 5 = -4k\] \[\displaystyle \Rightarrow k = -\left(\frac{\ln 2 - \ln 5 }{4}\right) \approx 0.229073 \]So now that we have computed the decay factor, we get that the exponential decay formula is
\[f(x) = \displaystyle A e^{-k x} = 5 e^{-\frac{\ln 2 - \ln 5 }{4} } \approx 3 e^{-0.229073 x} \]The following is obtained if we graphed this function:
More About Exponential Decay
The exponential decay is a model in which the exponential function plays a key role and is one very useful model that fits many real life application theories. The most famous application of exponential decay has to do with the behavior of radioactive materials.
Indeed, radioactive material follows an exponential decay equation, and each material has (depending on its own volatility) its half-time, which is the amount of time it takes for the amount of radioactive material to reduce to half.
Usually, the formula for radioactive decay is written as
\[A(t) =\displaystyle A_0 e^{-kt} \]or sometimes it is expressed in terms of the half-life \(h\) as
\[A(t) =\displaystyle A_0 e^{-\left(\frac{1}{h} \ln 2 \right)t}\]What does exponential decay mean?
Mathematically, a function has exponential decay if it can be written in the form \(f(x) = A e^{-kx}\). For many of you, this would not say too much.
Ok, that is fine, so we can describe the exponential decay. Having exponential decay, you may think, means "decaying REALLY fast". While function with exponential decay DO decay really fast, not all functions that decay really fast have exponential decay.
For example, consider \(f(x) = \frac{1}{x^2}\). If you graph this function, you will see it decays really fast, but it actually does not have exponential decay.
If you were to describe exponential decay, beyond the algebraic terms of its definition, you will need to say that a function has exponential decay if it decays really fast, but it ALSO has a crucial property:
Regardless the value of the function at a certain point \(x\), there exists a value \(h\) so that the value of the value of the function at the point \(x+h\) is half that of the value of the function at \(x\).
In order words, there is a constant value \(h\) (yes, you guessed, the half-life) that has the property that the function reduces its value to half after \(h\) units.
The function \(f(x) = \frac{1}{x^2}\), even though it decays fast, does not have the above (half-life) property.